题目内容
在平面内，如果用一条直线去截正方形的一个角，那么截下的一个直角三角形按图所标边长，由勾股定理有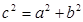
。设想正方形换成正方体，把截线换成如图所示的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥
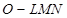，如果用
，
，
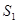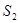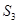表示三个侧面面积，
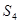表示截面面积，那么你类比得到的结论是 。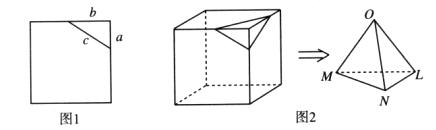
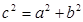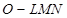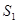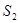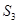。设想正方形换成正方体，把截线换成如图所示的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥，如果用，，表示三个侧面面积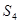，表示截面面积，那么你类比得到的结论是 。
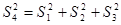
解：建立从平面图形到空间图形的类比，于是作出猜想：S42=S12+S22+S32
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
，
并猜测
的表达式；
＋
＋
＋…＋
．
，
则
边上的高
； 拓展到空间，如图，三棱锥
的三条侧棱SB、SB、SC两两相互垂直,且
,则点
到面
的距离
，第2个五角形数记作
，第3个五角形数记作
，第4个五角形数记作
，……，若按此规律继续下去，则
，若
，则
．
1 5 12 22
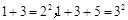猜想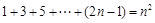
”是归纳推理
，经计算得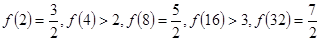
观察上式结果，可推测出一般结论 
，内切圆的半径为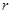
，则三角形的面积为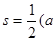
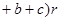；四面体的四个面的面积分别为
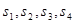，内切球的半径为
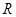．类比三角形的面积可得四面体的体积为（ ）
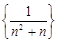依次按第一个括号一个数，第二个括号两
），（
，
），（
， 
，
），（
，
，
，
）,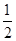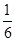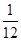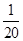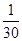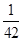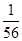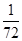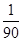