题目内容
某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1) 求出 ,
,

 并猜测
并猜测 的表达式;
的表达式;
(2) 求证: +
+ +
+ +…+
+…+
 .
.

(1) 求出
 ,
,

 并猜测
并猜测 的表达式;
的表达式;(2) 求证:
 +
+ +
+ +…+
+…+
 .
.
(1) f(2)=5,f(3)=13,f(4)=25,f(5)=25+4×4=41. f(n)=2n2-2n+1.
(2)略
(2)略
本试题主要是考查了数列的归纳猜想思想的运用,根据前几项。来猜想并运用数学归纳法加以证明。
(1)结合题目中的 递推关系式可知前几项的值,并猜想结论。
(2)分为两步骤进行,先证明n取第一个值时成立,再假设n=k时成立,证明n=k+1时也成立即可。
解析:(1)∵f(1)=1,f(2)=5,f(3)=13,f(4)=25,
∴f(5)=25+4×4=41.
(2)∵f(2)-f(1)=4=4×1,f(3)-f(2)=8=4×2,
f(4)-f(3)=12=4×3,f(5)-f(4)=16=4×4,
由上式规律得出f(n+1)-f(n)=4n.
∴f(n)-f(n-1)=4(n-1),f(n-1)-f(n-2)=4·(n-2),
f(n-2)-f(n-3)=4·(n-3),…
f(2)-f(1)=4×1,∴f(n)-f(1)=4[(n-1)+(n-2)+…+2+1]=2(n-1)·n,∴f(n)=2n2-2n+1(n≥2),又n=1时,f(1)也适合f(n).∴f(n)=2n2-2n+1.
(3)当n≥2时,==,
∴+++…+=1+
=1+=-.
(1)结合题目中的 递推关系式可知前几项的值,并猜想结论。
(2)分为两步骤进行,先证明n取第一个值时成立,再假设n=k时成立,证明n=k+1时也成立即可。
解析:(1)∵f(1)=1,f(2)=5,f(3)=13,f(4)=25,
∴f(5)=25+4×4=41.
(2)∵f(2)-f(1)=4=4×1,f(3)-f(2)=8=4×2,
f(4)-f(3)=12=4×3,f(5)-f(4)=16=4×4,
由上式规律得出f(n+1)-f(n)=4n.
∴f(n)-f(n-1)=4(n-1),f(n-1)-f(n-2)=4·(n-2),
f(n-2)-f(n-3)=4·(n-3),…
f(2)-f(1)=4×1,∴f(n)-f(1)=4[(n-1)+(n-2)+…+2+1]=2(n-1)·n,∴f(n)=2n2-2n+1(n≥2),又n=1时,f(1)也适合f(n).∴f(n)=2n2-2n+1.
(3)当n≥2时,==,
∴+++…+=1+
=1+=-.

练习册系列答案
相关题目
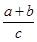 =
=  +
+ ”
”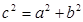 。设想正方形换成正方体,把截线换成如图所示的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥
。设想正方形换成正方体,把截线换成如图所示的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥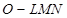 ,如果用
,如果用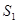 ,
,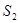 ,
,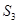 表示三个侧面面积,
表示三个侧面面积,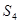 表示截面面积,那么你类比得到的结论是 。
表示截面面积,那么你类比得到的结论是 。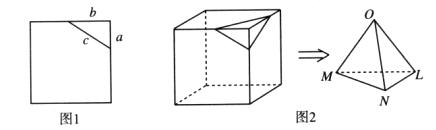
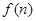 条对角线,则凸n+l边形的对角线的条数
条对角线,则凸n+l边形的对角线的条数 )为 ( )
)为 ( )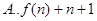


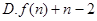
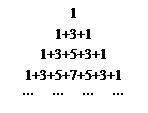
 满足:对任意的
满足:对任意的 ,只有有限个正整数
,只有有限个正整数 使得
使得 成立,记这样的
成立,记这样的 ,则得到一个新数列
,则得到一个新数列 。例如,若数列
。例如,若数列 ,…,则数列
,…,则数列 , ….已知对任意的
, ….已知对任意的 ,则
,则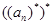 = 。
= 。