题目内容
两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图1中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作 ,第2个五角形数记作
,第2个五角形数记作 ,第3个五角形数记作
,第3个五角形数记作 ,第4个五角形数记作
,第4个五角形数记作 ,……,若按此规律继续下去,则
,……,若按此规律继续下去,则 ,若
,若 ,则
,则 .
.

 1 5 12 22
1 5 12 22
 ,第2个五角形数记作
,第2个五角形数记作 ,第3个五角形数记作
,第3个五角形数记作 ,第4个五角形数记作
,第4个五角形数记作 ,……,若按此规律继续下去,则
,……,若按此规律继续下去,则 ,若
,若 ,则
,则 .
.
 1 5 12 22
1 5 12 22
35,10
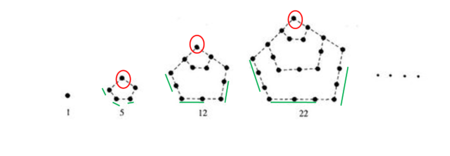
将图中的小石子分组,分组方法如图所示
1+(3*1+1)+(3*2+1)+(3*3+1)+…+【3*(n-1)+1】=
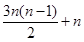
 .
.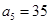 a(n)=145时,n=10.
a(n)=145时,n=10.
练习册系列答案
相关题目
 上分别存在点
上分别存在点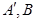 与
与 ,则三角形面积之比
,则三角形面积之比  ,如图若不在同一平面内的射线
,如图若不在同一平面内的射线 和
和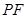 上分别存在点
上分别存在点 点
点 和点
和点
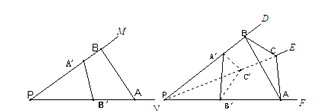
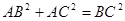 。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为 .
。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为 .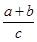 =
=  +
+ ”
”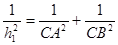 ;类比此性质,如图,在四面体P—ABC中,若PA,PB,PC两两垂直,底面ABC上的高为h,则h与PA, PB, PC有关系式: .
;类比此性质,如图,在四面体P—ABC中,若PA,PB,PC两两垂直,底面ABC上的高为h,则h与PA, PB, PC有关系式: .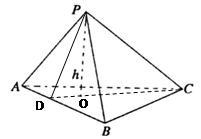
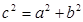 。设想正方形换成正方体,把截线换成如图所示的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥
。设想正方形换成正方体,把截线换成如图所示的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥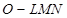 ,如果用
,如果用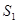 ,
,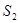 ,
,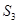 表示三个侧面面积,
表示三个侧面面积,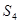 表示截面面积,那么你类比得到的结论是 。
表示截面面积,那么你类比得到的结论是 。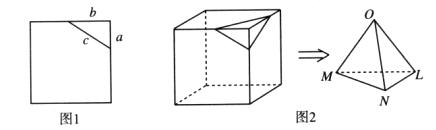
 ,三边长为
,三边长为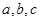 ,则三角形的面积等于
,则三角形的面积等于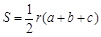 ,根据类比推理的方法,若一个四面体的内切球的半径为
,根据类比推理的方法,若一个四面体的内切球的半径为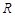 ,四个面的面积分别是
,四个面的面积分别是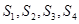 ,则四面体的体积
,则四面体的体积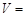 _____
_____  满足:对任意的
满足:对任意的 ,只有有限个正整数
,只有有限个正整数 使得
使得 成立,记这样的
成立,记这样的 ,则得到一个新数列
,则得到一个新数列 。例如,若数列
。例如,若数列 ,…,则数列
,…,则数列 , ….已知对任意的
, ….已知对任意的 ,则
,则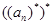 = 。
= 。