题目内容
【题目】已知椭圆C:![]() (
(![]() )的左,右焦点为
)的左,右焦点为![]() ,
,![]() ,且焦距为
,且焦距为![]() ,点
,点![]() ,
,![]() 分别为椭圆C的上、下顶点,满足
分别为椭圆C的上、下顶点,满足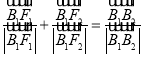 .
.
(1)求椭圆C的方程;
(2)已知点![]() ,椭圆C上的两个动点M,N满足
,椭圆C上的两个动点M,N满足![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)设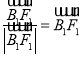 ,
,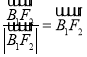 ,
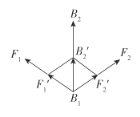
,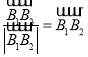 ,结合已知的向量表达式,根据平面向量加法的几何意义可知四边形
,结合已知的向量表达式,根据平面向量加法的几何意义可知四边形![]() 为菱形,结合已知条件进行求解即可;
为菱形,结合已知条件进行求解即可;
(2)根据直线![]() 是否存在斜率进行分类讨论.设直线
是否存在斜率进行分类讨论.设直线![]() 的方程,与椭圆方程联立,结合一元二次方程根与系数的关系,结合两平面向量垂直的性质进行求解即可.
的方程,与椭圆方程联立,结合一元二次方程根与系数的关系,结合两平面向量垂直的性质进行求解即可.
(1)设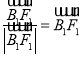 ,
,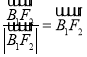 ,
,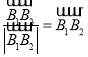 ,
,
由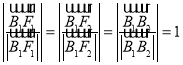 可知四边形
可知四边形![]() 为菱形且
为菱形且![]() ,
,
故![]() ,解得
,解得![]() ,故
,故![]() ,
,
椭圆C的方程为![]() .
.
(2)当直线![]() 斜率存在时,设
斜率存在时,设![]() :
:![]() ,
,![]() ,
,![]() .
.
联立![]() 消去y得
消去y得
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
由![]() ,则
,则![]() ,
,
即![]() ,
,
整理得![]() ,
,
将![]() ,
,![]() 代入整理得
代入整理得![]() ,
,
即![]() ,
,
解得![]() 或
或![]() .
.
当![]() 时,直线
时,直线![]() :
:![]() 过点E,舍去;
过点E,舍去;
当![]() 时,直线
时,直线![]() :
:![]() 过定点
过定点![]() .
.
当直线![]() 斜率不存在时,不妨设
斜率不存在时,不妨设![]() ,
,![]() ,
,
则由![]() ,则
,则![]() ,
,
即![]() ,即
,即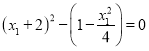 ,
,
即![]() ,解得
,解得![]() (舍去)或
(舍去)或![]() ,也过定点
,也过定点![]() .
.
综上,直线![]() 过定点
过定点![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目