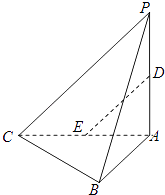Question

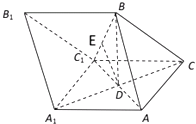
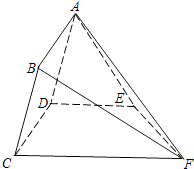
【题目】如图，矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角，DE∥CF，CD⊥DE，AD=2， ，CF=6，∠CFE=45°．
（Ⅰ）求证：BF∥平面ADE；
（Ⅱ）在线段CF上求一点G，使锐二面角B﹣EG﹣D的余弦值为 ．

Answer 1

【答案】证明：（Ⅰ）∵在矩形ABCD中BC∥AD，
AD平面ADE
BC平面ADE，
∴BC∥平面ADE，
同理CF∥平面ADE，
又∵BC∩CF=C，
∴平面BCF∥平面ADE，
而BF平面BCF，
∴BF∥平面ADE．
（Ⅱ）∵CD⊥AD，CD⊥DE
∴∠ADE即为二面角A﹣CD﹣F的平面角，
∴∠ADE=60°
又∵AD∩DE=D，
∴CD⊥平面ADE，
又∵CD平面CDEF
∴平面CDEF⊥平面ADE，
作AO⊥DE于O，则AO⊥平面CDEF．
连结CE，
在△CEF中由余弦定理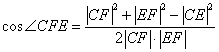
，
即
∴ ，
易求得，∠ECF=45°，CD=DE=3，OD=1，OE=2．
以O为原点，以平行于DC的直线为x轴，以直线DE为y轴，建立如图空间直角坐标系O﹣xyz，
则 ，C（3，﹣1，0），E（0，2，0），F（3，5，0），
设G（3，t，0），﹣1≤t≤5，
则 ，
，
设平面BEG的一个法向量为 ，
则由 ，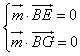
得 ，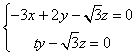
取 ，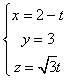
得 ．
平面DEG的一个法向量 ，
∴ ．
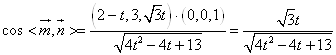为使锐二面角B﹣EG﹣D的余弦值为 ，
只需 ，
解得 ，
此时 ．
∴G（3， ，0）．
即所求的点G为线段CF的靠近C端的四分之一分点．

【解析】（1）利用平面与平面平行的判定定理证明平面BCF∥平面ADE，从而得到BF∥平面ADE．（Ⅱ）利用直线与平面，平面与平面垂直的判定定理证明平面CDEF⊥平面ADE，根据平面与平面垂直的性质定理可知，作AO⊥DE于O，则AO⊥平面CDEF．建立如图所示空间直角坐标系，写出点的坐标，利用平面法向量以及锐二面角B﹣EG﹣D的余弦值确定G点的坐标，从而确定点G的位置．
【考点精析】通过灵活运用直线与平面平行的判定，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行即可以解答此题．