Question

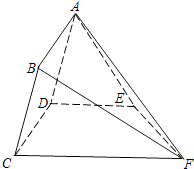
【题目】如图，在三棱锥中， ， 底面， ，且.

（1）若为上一点，且，证明:平面平面.

（2）若为棱上一点，且平面，求三棱锥的体积.

Answer 1

【答案】（1）见解析；（2）

【解析】试题分析：（1）由平面可得，又， ，所以平面，根据面面垂直的判定定理得平面平面。（2）在中，由余弦定理得

，根据勾股定理可得AB=3，BC=1，PB=2，由平面可得，从而得到，故BD=1.过作，交于，则为三棱锥的高，且由三棱锥的体积公式可得。

试题解析：

（1）证明：∵ 平面， 平面

∴.

又， ，

∴平面.

∵平面，

∴ 平面平面.

（2）解：

在中，由余弦定理得

,

∴，

由条件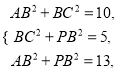得 解得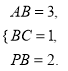

∵平面， 平面，平面平面，

∴，

∴.

过作，交img src="https://thumb.zyjl.cn/questionBank/Upload/2017/12/29/18/b0e15a69/SYS201712291828428337502978_DA/SYS201712291828428337502978_DA.053.png" width="28" height="17" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />于，则为三棱锥的高，则.

∵，

∴ .

即三棱锥的体积为。