题目内容
已知函数 .
.
(Ⅰ)讨论函数 的单调性;
的单调性;
(Ⅱ)设 ,证明:对任意
,证明:对任意 ,
, .
.
(Ⅰ)分类讨论得到单调性 (Ⅱ)构造函数用导数的方法证明.
解析试题分析:(Ⅰ) f(x)的定义域为(0,+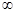 ),
),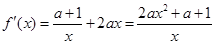
当a≥0时,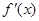 >0,故f(x)在(0,+
>0,故f(x)在(0,+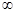 )单调增加;
)单调增加;
当a≤-1时,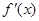 <0, 故f(x)在(0,+
<0, 故f(x)在(0,+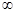 )单调减少;
)单调减少;
当-1<a<0时,令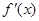 =0,解得x=
=0,解得x=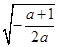 .当x∈(0,
.当x∈(0, 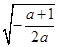 )时,
)时, 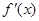 >0;
>0;
x∈(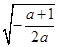 ,+
,+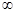 )时,
)时,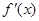 <0, 故f(x)在(0,
<0, 故f(x)在(0, 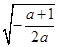 )单调增加,在(
)单调增加,在(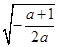 ,+
,+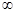 )单调减少
)单调减少
(Ⅱ)不妨设x1≥x2.由于a≤-2,故f(x)在(0,+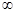 )单调减少.
)单调减少.
所以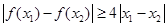 等价于
等价于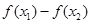 ≥4x1-4x2,
≥4x1-4x2,
即f(x2)+ 4x2≥f(x1)+ 4x1.
令g(x)=f(x)+4x,则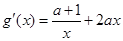 +4=
+4=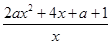 .
.
于是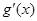 ≤
≤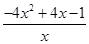 =
=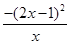 ≤0.
≤0.
从而g(x)在(0,+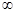 )单调减少,故g(x1) ≤g(x2),即 f(x1)+ 4x1≤f(x2)+ 4x2,
)单调减少,故g(x1) ≤g(x2),即 f(x1)+ 4x1≤f(x2)+ 4x2,
故对任意x1,x2∈(0,+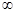 ) ,
) ,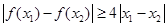 .
.
考点:利用导数求闭区间上函数的最值;利用导数研究函数的单调性.
点评:本题考查利用导数研究函数的单调性及函数的最值问题,考查分类讨论思想,考查学生综合运用知识分析问题解决问题的能力,属难题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
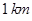 的等边三角形
的等边三角形 的顶点
的顶点 处(如图),现要在边
处(如图),现要在边 上的
上的 点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返
点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返 车间5次,往返
车间5次,往返 车间20次,设叉车每天往返的总路程为
车间20次,设叉车每天往返的总路程为 .(注:往返一次即先从仓库到车间再由车间返回仓库)
.(注:往返一次即先从仓库到车间再由车间返回仓库)
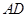 长为
长为 ,将
,将 表示成
表示成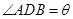 ,将
,将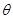 的函数关系式.
的函数关系式.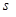 的最小值,并指出点
的最小值,并指出点 是定义在
是定义在 上的偶函数,且
上的偶函数,且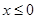 时,
时, .
. 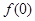 ,
,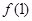 ;
;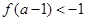 ,求
,求 的取值范围.
的取值范围.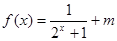 ,
,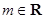 .
.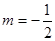 ,求证:函数
,求证:函数 是
是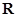 上的奇函数;
上的奇函数;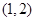 上没有零点,求实数
上没有零点,求实数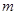 的取值范围.
的取值范围.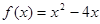 ,
,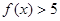 ,求
,求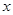 的范围; (2)不等式
的范围; (2)不等式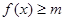 对任意
对任意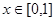 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。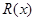 万元,且
万元,且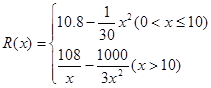 .
.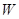 (万元)关于年产品(千件)的函数解析式;
(万元)关于年产品(千件)的函数解析式;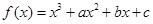 ,曲线
,曲线 在点
在点 处的切线为
处的切线为 ,若
,若 时,
时, 的值;
的值; 上的最大值和最小值.
上的最大值和最小值.
 ;
; 的解集为空集,求
的解集为空集,求 的取值范围.
的取值范围.