题目内容
某工厂修建一个长方体无盖蓄水池，其容积为4 800立方米，深度为3米．池底每平方米的造价为150元，池壁每平方米的造价为120元．设池底长方形长为x米．
（1）求底面积，并用含x的表达式表示池壁面积；
（2）怎样设计水池能使总造价最低?最低造价是多少?
(1) s=1600，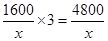 
(2) x="40," 最低造价268800
解析试题分析：（1）根据题意，由于修建一个长方体无盖蓄水池，其容积为4 800立方米，深度为3米．可得底面积为1600，池壁面积；s=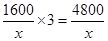（2）同时池底每平方米的造价为150元，池壁每平方米的造价为120元．设池底长方形长为x米，则可知总造价s=
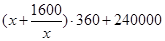,x=40时则
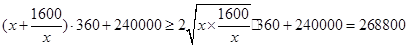.故可知当x=40时，则有可使得总造价最低。最低造价师268800元.
考点：不等式求解最值
点评：主要是考查了不等式求解最值的运用，属于基础题。
练习册系列答案
相关题目
，
．
的解集；
的不等式
在
的取值范围．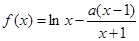
（
，
），
．
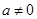的单调区间,并确定其零点个数；
在其定义域内单调递增，求
的取值范围；
（
）．
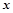（单位：辆/千米）的函数，当桥上的车流密度达到200辆/千米时，造成堵塞，此时车速度为0；当车流密度不超过20辆/千米时，车流速度为60千米,/小时，研究表明：当
时，车流速度v是车流密度
时，求函数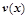
的表达式；
可以达到最大，并求出最大值.（精确到1辆/小时）
.
的单调性； 
，证明：对任意
，
.
的二次项系数为
，满足不等式
的解集为（1，3），且方程
有两个相等的实根，求
个单位的固体碱在水中逐渐溶化,水中的碱浓度
与时间
(小时)的关系可近似地表示为：
,只有当污染河道水中碱的浓度不低于
时,才能对污染产生有效的抑制作用.
,求
%，则销售量将减少
%，且该化工产品每吨的价格上涨幅度不超过
%，
其中
为正常数
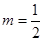时，该产品每吨的价格上涨百分之几，可使销售的总金额最大？
，当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0千米/小时． 
）