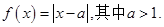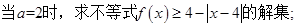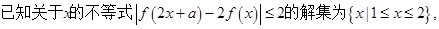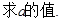题目内容
已知函数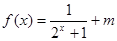 ,
,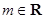 .
.
(1)若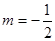 ,求证:函数
,求证:函数 是
是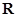 上的奇函数;
上的奇函数;
(2)若函数 在区间
在区间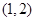 上没有零点,求实数
上没有零点,求实数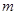 的取值范围.
的取值范围.
(1 )定义域为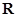 关于原点对称.证明
关于原点对称.证明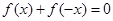 。(2)
。(2)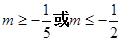 。
。
解析试题分析:(1 )定义域为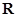 关于原点对称.
关于原点对称.
因为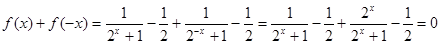 ,
,
所以函数 是定义在
是定义在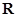 上的奇函数
上的奇函数
(2)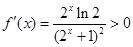
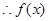 是实数集
是实数集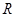 上的单调递增函数(不说明单调性扣2分)又函数
上的单调递增函数(不说明单调性扣2分)又函数 的图象不间断,在区间
的图象不间断,在区间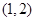 恰有一个零点,有
恰有一个零点,有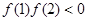
即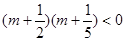 解之得
解之得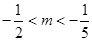 ,故函数
,故函数 在区间
在区间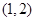 没有零点时,实数
没有零点时,实数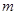 的取值范围是
的取值范围是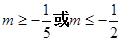 14分
14分
考点:函数的奇偶性、单调性,函数的零点,简单不等式解法。
点评:中档题,研究函数的奇偶性,一般利用定义法,注意定义域关于原点对称。研究函数的单调性,可以利用定义法、导数法。在指定区间,导函数值非负,函数为增函数,导函数值非正,函数为减函数。利用函数零点存在定理,确定m的不等式。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 .设某商品标价为
.设某商品标价为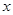 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为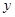 .
. 时,
时,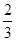 ?
?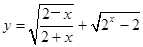 的定义域为
的定义域为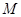 ,
, 时,求函数
时,求函数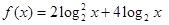 的最大值。
的最大值。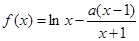 (
( ,
,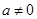 ),
), .
. 的单调区间,并确定其零点个数;
的单调区间,并确定其零点个数; 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围; (
( ).
).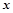 (单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当
(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当 时,车流速度v是车流密度
时,车流速度v是车流密度 时,求函数
时,求函数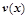 的表达式;
的表达式; 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时) .
. 的单调性;
的单调性;  ,证明:对任意
,证明:对任意 ,
, .
. 个单位的固体碱在水中逐渐溶化,水中的碱浓度
个单位的固体碱在水中逐渐溶化,水中的碱浓度 与时间
与时间 (小时)的关系可近似地表示为:
(小时)的关系可近似地表示为: ,只有当污染河道水中碱的浓度不低于
,只有当污染河道水中碱的浓度不低于 时,才能对污染产生有效的抑制作用.
时,才能对污染产生有效的抑制作用. ,求
,求 在
在 处取得极小值.
处取得极小值. 的值;
的值; 在
在 处的切线方程为
处的切线方程为 ,求证:当
,求证:当 时,曲线
时,曲线 不可能在直线
不可能在直线