题目内容
抛物线y2=2Px,过点A(2,4),F为焦点,定点B的坐标为(8,-8),则|AF|∶|BF|值为
| A.1∶4 | B.1∶2 | C.2∶5 | D.3∶8 |
C
解析试题分析:因为抛物线y2=2Px,过点A(2,4),F为焦点,那么可知16=4p,p=4,可知其方程为y2=8x,则利用抛物线定义得到BF=10和AF=4的长度,那么可知距离的比值为2:5,故选C.
考点:本试题考查了抛物线的性质运用。
点评:解决抛物线的问题,一般都要考查其定义的运用,也就是抛物线上任意一点到其焦点的距离等于其到准线的距离来表示焦半径的长度,属于基础题。

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知 是以
是以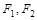 为焦点的椭圆
为焦点的椭圆 上的一点,若
上的一点,若
 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
A. | B. | C. | D. |
已知 是椭圆
是椭圆 的两个焦点,
的两个焦点,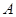 为椭圆上的一点,且
为椭圆上的一点,且 ,则
,则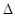
 的面积是( )
的面积是( )
| A.7 | B. | C. | D. |
抛物线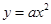 的焦点坐标是( )
的焦点坐标是( )
A. | B.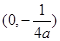 | C. | D. |
设抛物线的顶点在原点,焦点与椭圆 的右焦点重合,则此抛物线的方程是( )
的右焦点重合,则此抛物线的方程是( )
| A.y2=-8x | B.y2=-4x | C.y2="8x" | D.y2=4x |
 (a>b>0)的两个焦点,过F2作椭圆的弦AB,若△AF1B的周长为16,椭圆的离心率
(a>b>0)的两个焦点,过F2作椭圆的弦AB,若△AF1B的周长为16,椭圆的离心率 ,则椭圆的方程为( )
,则椭圆的方程为( )



 的左焦点
的左焦点 引圆
引圆 的切线,切点为
的切线,切点为 ,延长
,延长 交双曲线右支于
交双曲线右支于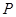 点,若
点,若 为线段
为线段 的中点,
的中点, 为坐标原点,则
为坐标原点,则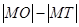 与
与 的大小关系为 ( )
的大小关系为 ( ) 

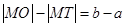

 中,
中, 为椭圆
为椭圆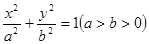 的四个顶点,F为其右焦点,直线
的四个顶点,F为其右焦点,直线 与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为
与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为



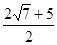
 ,
, 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过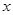 轴的直线与双曲线交于
轴的直线与双曲线交于 ,
, 两点,若△
两点,若△ 是锐角三角形,则该双曲线离心率的取值范围是( )
是锐角三角形,则该双曲线离心率的取值范围是( )


