题目内容
(本小题满分14分)有人玩掷正四面体骰子走跳棋的游戏,已知正四面体骰子四个面上分别印有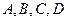 ,棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次骰子,若掷出后骰子为
,棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次骰子,若掷出后骰子为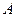 面,棋子向前跳2站,若掷出后骰子为
面,棋子向前跳2站,若掷出后骰子为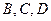 中的一面,则棋子向前跳1站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为
中的一面,则棋子向前跳1站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为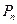 (
(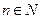 ).
).
(Ⅰ)求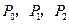 ;
;
(Ⅱ)求证: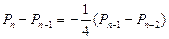 ;
;
(Ⅲ)求玩该游戏获胜的概率.
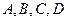 ,棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次骰子,若掷出后骰子为
,棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次骰子,若掷出后骰子为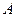 面,棋子向前跳2站,若掷出后骰子为
面,棋子向前跳2站,若掷出后骰子为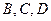 中的一面,则棋子向前跳1站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为
中的一面,则棋子向前跳1站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为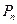 (
(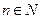 ).
).(Ⅰ)求
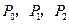 ;
;(Ⅱ)求证:
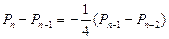 ;
;(Ⅲ)求玩该游戏获胜的概率.
解:(1)依题意,得
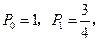 .………………………………………2分
.………………………………………2分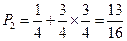 ……………………………………………………4分
……………………………………………………4分(Ⅱ)设棋子跳到第n站(2≤n≤99)有两种可能:第一种,棋子先到第
 站,又掷出后得到A面,其概率为
站,又掷出后得到A面,其概率为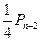 ;第二种,棋子先到第
;第二种,棋子先到第 站,又掷出后得到
站,又掷出后得到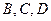 中的一面,其概率为
中的一面,其概率为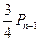 ,由于以上两种可能是互斥的,所以
,由于以上两种可能是互斥的,所以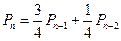 ,
,即有
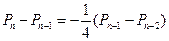 .………………………………………………………………9分
.………………………………………………………………9分(Ⅲ)由(Ⅱ)知数列
 是首项为
是首项为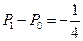 ,公比为
,公比为 的等比数列.
的等比数列.于是有
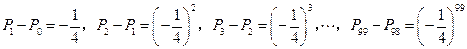 .
.把以上各式相加,得
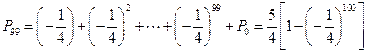 .
.因此,获胜的概率为
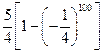 .………………………………………………14分
.………………………………………………14分略

练习册系列答案
相关题目
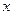 表示第
表示第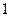 枚骰子出现的点数,
枚骰子出现的点数,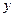 表示第
表示第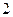 枚骰子出现的点数。设点P的坐标为
枚骰子出现的点数。设点P的坐标为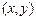 。
。 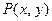 在直线
在直线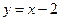 上的概率;
上的概率;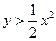 的概率
的概率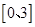 上任投一点,则此点坐标大于2的概率为( )
上任投一点,则此点坐标大于2的概率为( )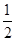
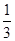
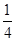
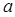 的正方形木板,它的四个角的空白部分都是以正方形
的正方形木板,它的四个角的空白部分都是以正方形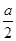 的圆孤,某人向此板投镖,假设每次都能击中木板,且击
的圆孤,某人向此板投镖,假设每次都能击中木板,且击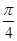
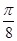
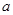 的取值有关
的取值有关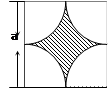
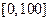 上是等可能出现的.单项80分以上,且总分170分以上才合格,求他合格的概率。
上是等可能出现的.单项80分以上,且总分170分以上才合格,求他合格的概率。 若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三
若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三 人合格的概率依次为0.5、0.6、0.4,第二次选拔,甲、乙、丙三人合格的概率依次为0.6、0.5、0.5。
人合格的概率依次为0.5、0.6、0.4,第二次选拔,甲、乙、丙三人合格的概率依次为0.6、0.5、0.5。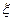 ,求
,求
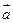 与向量
与向量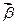 ,其满足
,其满足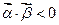 的概率是 ( )
的概率是 ( )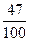
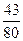
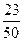
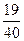
 形的顶点为圆心,半径为1的圆弧,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是 .
形的顶点为圆心,半径为1的圆弧,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是 . 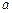 , 第二次得到的数值为
, 第二次得到的数值为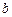 , 将它们作为关于
, 将它们作为关于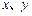 的二元一次方程组
的二元一次方程组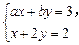 的系数, 则方程组有唯一解的概率为 (用数字作答)
的系数, 则方程组有唯一解的概率为 (用数字作答)