题目内容
19．求证：f（x）=x+$\frac{{a}^{2}}{x}$（a∈R+）在区间（0，a]上是减函数．分析 利用减函数的定义即可证明．
解答 证明：任取x1，x2∈（0，a]，且x1＜x2，
则f（x1）-f（x2）=（x1+$\frac{{a}^{2}}{{x}_{1}}$）-（x2+$\frac{{a}^{2}}{{x}_{2}}$）=$\frac{{（x}_{1}{-x}_{2}）{{（x}_{1}x}_{2}{-a}^{2}）}{{{x}_{1}x}_{2}}$，
∵0＜x1＜x2≤a，∴x1-x2＜0，x1x2-a2＜0，x1x2＞0，
∴f（x1）-f（x2）＞0，即f（x1）＞f（x2），
∴f（x）在区间（0，a]上是减函数
点评 正确理解函数的单调性的定义和熟练掌握证明函数单调性的方法步骤是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
10．
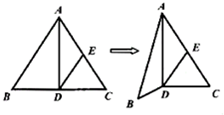如图，已知DE是正△ABC的中位线，沿AD将△ABC折成直二面角B-AD-C，则翻折后异面直线AB与DE所成角的余弦值为（ ）
如图，已知DE是正△ABC的中位线，沿AD将△ABC折成直二面角B-AD-C，则翻折后异面直线AB与DE所成角的余弦值为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | 0 |
4．已知过双曲线x2-y2=2的左焦点作直线l与双曲线交于A，B两点．且|AB|=4，则这样的直线有（ ）
| A． | 1条 | B． | 2条 | C． | 3条 | D． | 4条 |
