题目内容

【题目】平面直角坐标系中，直线的参数方程为，（为参数）.以原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（1）写出直线的极坐标方程与曲线的直角坐标方程；

（2）已知与直线平行的直线过点，且与曲线交于两点，试求.

【答案】(1)直线的极坐标方程为，曲线的直角坐标方程为.(2).

【解析】试题分析：（1）先利用加减消元法将直线的参数方程化为直角坐标方程，再利用，得直线的极坐标方程，最后根据，将曲线的极坐标方程化为直角坐标方程，（2）先根据点斜式写出直线方程，与抛物线方程联立，利用韦达定理以及弦长公式求.

试题解析：（1）将，代入直线方程得，

由可得，

曲线的直角坐标方程为.

（2）直线的倾斜角为，∴直线的倾斜角也为，又直线过点，

∴直线的参数方程为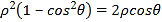（为参数），将其代入曲线的直角坐标方程可得

，设点对应的参数分别为.

由一元二次方程的根与系数的关系知，，

∴ .

练习册系列答案
相关题目

【题目】已知函数.

(1)若，求函数的单调区间；

(2)若的极小值点，求实数a的取值范围。

【题目】某同学用“五点法”画函数在某一周期内的图象时，列表并填入了部分数据，如下表：

①

（1）请将上面表格中①的数据填写在答题卡相应位置上，并直接写出函数的解析式；

（2）若将函数的图象上所有点的横坐标变为原来的倍，纵坐标不变，得到函数的图象，求当时，函数的单调递增区间；

（3）若将函数图象上的所有点向右平移个单位长度，得到的图象. 若图象的一个对称中心为，求的最小值.

【题目】已知数列， 都是单调递增数列，若将这两个数列的项按由小到大的顺序排成一列（相同的项视为一项），则得到一个新数列.

（1）设数列、分别为等差、等比数列，若， ， ，求；

（2）设的首项为1，各项为正整数， ，若新数列是等差数列，求数列 的前项和；

（3）设（是不小于2的正整数），，是否存在等差数列，使得对任意的，在与之间数列的项数总是？若存在，请给出一个满足题意的等差数列；若不存在，请说明理由.

【题目】设函数．

（1）若是偶函数，求的值；

（2）若存在，使得成立，求实数的取值范围；

（3）设函数，若在有零点，求实数的取值范围．

【题目】已知正数数列{an}的前n项和为Sn，满足 ，.

（1）求数列{an}的通项公式；

（2）设，若是递增数列，求实数a的取值范围．

【题目】从5名男生和4名女生中选出4人去参加座谈会，问：

(1)如果4人中男生和女生各选2人，有多少种选法？

(2)如果男生中的甲与女生中的乙至少要有1人在内，有多少种选法？

(3)如果4人中必须既有男生又有女生，有多少种选法？

【题目】如图，已知椭圆的离心率为，过左焦点且斜率为的直线交椭圆于， 两点，线段的中点为，直线交椭圆于， 两点．

（I）求椭圆的方程．

（II）求证：点在直线上．

（III）是否存在实数，使得的面积是面积的倍？若存在，求出的值．若不存在，说明理由．

【题目】选修4-4：坐标系与参数方程

在平面直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，曲线C的极坐标方程为.

（1）求曲线的普通方程和的直角坐标方程；

（2）设分别交于点，求的面积.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网