题目内容
16.对于任意x、y∈R,值域都为正,f(xy)=f(x)f(y),求f(x)的奇偶性.分析 利用赋值法,结合函数奇偶性的定义进行判断即可.
解答 解:令x=y=1得,f(1)=f(1)•f(1),其f(1)>0,
所以f(1)=1,
再令x=y=-1,得f(-1)=1,
再令y=-1得,f(-x)=f(-1)f(x)=f(x),
所以f(x)为偶函数.
点评 本题主要考查函数奇偶性的判断,利用抽象函数的关系以及函数奇偶性的定义是解决本题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
6.已知曲线P:y=e3x,曲线Q:y=lnx${\;}^{\frac{1}{3}}$,则曲线P与曲线Q( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于y=x对称 |
4.为了考察两个变量x和y之间的线性相关性,甲、乙两个同学各自独立地作10次和15次试验,并且利用线性回归方法,求得回归直线分别为l1和l2.已知在两个人的试验中发现对变量x的观测数据的平均值恰好相等,都为s,对变量y的观测数据的平均值也恰好相等,都为t.那么下列说法正确的是( )
| A. | 直线l1和l2相交,但是交点未必是点(s,t) | |
| B. | 直线l1和l2有交点(s,t) | |
| C. | 直线l1和l2由于斜率相等,所以必定平行 | |
| D. | 直线l1和l2必定重合 |
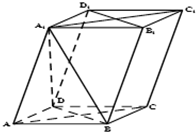 如图,平行六面体体ABCD-A1B1C1D1中,所有棱长均为1,且∠BAD=∠A1AB=∠A1AC=60°.
如图,平行六面体体ABCD-A1B1C1D1中,所有棱长均为1,且∠BAD=∠A1AB=∠A1AC=60°.