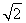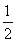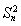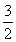题目内容
设向量a=(2,sin θ),b=(1,cos θ),θ为锐角.
(1)若a·b=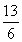 ,求sin θ+cos θ的值;
,求sin θ+cos θ的值;
(2)若a∥b,求sin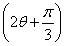 的值.
的值.
(1)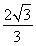 (2)
(2)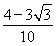
【解析】(1)因为a·b=2+sin θcos θ=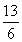 ,
,
所以sin θcos θ=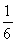 .(2分)
.(2分)
所以(sin θ+cos θ)2=1+2sin θcos θ=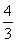 .
.
又因为θ为锐角,所以sin θ+cos θ=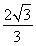 .(5分)
.(5分)
(2)法一:因为a∥b,所以tan θ=2.(7分)
所以sin 2θ=2sin θcos θ= ,cos 2θ=cos2θ-sin2θ=
,cos 2θ=cos2θ-sin2θ=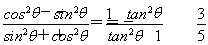 .(11分)
.(11分)
所以sin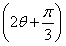 =
=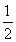 sin 2θ+
sin 2θ+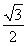 cos 2θ=
cos 2θ=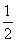 ×
×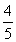 +
+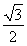 ×
×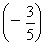 =
=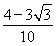 .(14分)
.(14分)
法二 因为a∥b,所以tan θ=2.(7分)
所以sin θ=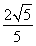 ,cos θ=
,cos θ=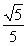 .
.
因此sin 2θ=2sin θcos θ=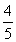 ,
,
cos 2θ=cos2θ-sin2θ=-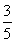 .(11分)
.(11分)
所以sin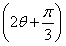 =
=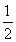 sin 2θ+
sin 2θ+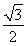 cos 2θ=
cos 2θ=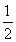 ×
×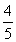 +
+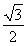 ×
×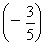 =
=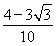 .
.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目