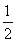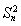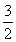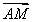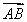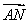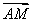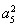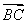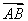题目内容
在△ABC中，角A，B，C的对边分别是a，b，c，a＝8，b＝10，△ABC的面积为20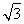
，则△ABC的最大角的正切值是________．
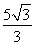或－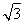
【解析】由题意可以求出sin C，得到∠C有两解，借助余弦定理分别求出三角形中最大角的正切值．由S△ABC＝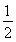
absin C，代入数据解得sin C＝
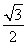，又∠C为三角形的内角，所以C＝60°或120°.若C＝60°，则在△ABC中，由余弦定理得c2＝a2＋b2－2abcos C＝84，此时，最大边是b，故最大角为∠B，其余弦值cos B＝
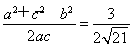，正弦值sin B＝
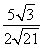，正切值tan B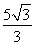＝；若C＝120°，此时，C为最大角，其正切值为tan 120°＝－.
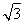练习册系列答案
相关题目
