题目内容
1.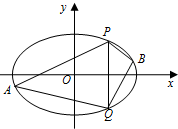 已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.(Ⅰ)求椭圆C的方程;
(Ⅱ)点P(2,3),Q(2,-3)在椭圆上,A、B是椭圆上位于直线PQ两侧的动点.
①若直线AB的斜率为$\frac{1}{2}$,求四边形APBQ面积的最大值;
②当A、B运动时,满足于∠APQ=∠BPQ,试问直线AB的斜率是否为定值?若是,请求出定值,若不是,请说明理由.
分析 (Ⅰ)由题意,椭圆一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点,可得出椭圆半短轴的长,再由$\frac{c}{a}=\frac{1}{2},{a^2}={c^2}+{b^2}$,即可求出a的值,从而得出椭圆的方程;
(Ⅱ)①设直线AB的方程,将直线方程和椭圆方程联立,通过消元,转化为一元二次方程去解决,求出弦AB的长,进而求出四边形的面积函数,求出面积的最大值,
②.当∠APQ=∠BPQ,则PA、PB的斜率之和为0,设直线PA的斜率为k,则PB的斜率为-k,PA的直线方程为y-3=k(x-2),将其与椭圆方程联立整理得(3+4k2)x2+8(3-2k)kx+4(3-2k)2-48=0,可得${x_1}+2=\frac{8(2k-3)k}{{3+4{k^2}}}$,同理PB的直线方程为y-3=-k(x-2),可得${x_2}+2=\frac{8k(2k+3)}{{3+4{k^2}}}$,${x_1}+{x_2}=\frac{{16{k^2}-12}}{{3+4{k^2}}},{x_1}-{x_2}=\frac{-48k}{{3+4{k^2}}}$,${k_{AB}}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{{k({x_1}+{x_2})-4k}}{{{x_1}-{x_2}}}$,化简即可求得AB的斜率为定值.
解答 解:(Ⅰ)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$椭圆的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点,可知$b=2\sqrt{3}$.
又$\frac{c}{a}=\frac{1}{2},{a^2}={c^2}+{b^2}$,解得a=4,c=2,
∴椭圆C的方程是$\frac{x^2}{16}+\frac{y^2}{12}=1$.
(II)①解:设A(x1,y1),B(x2,y2),直线AB的方程为$y=\frac{1}{2}x+t$,代入$\frac{x^2}{16}+\frac{y^2}{12}=1$,
得x2+tx+t2-12=0由△>0,解得-4<t<4
由韦达定理得${x_1}+{x_2}=-t,{x_1}{x_2}={t^2}-12$.
四边形APBQ的面积$S=\frac{1}{2}×6×|{{x_1}-{x_2}}|=3\sqrt{48-3{t^2}}$
∴当t=0,${S_{max}}=12\sqrt{3}$.
②解:当∠APQ=∠BPQ,则PA、PB的斜率之和为0,设直线PA的斜率为k
则PB的斜率为-k,PA的直线方程为y-3=k(x-2),
由$\left\{\begin{array}{l}y-3=k(x-2)…(1)\\ \frac{x^2}{16}+\frac{y^2}{12}=1…(2)\end{array}\right.$得(3+4k2)x2+8(3-2k)kx+4(3-2k)2-48=0,可得${x_1}+2=\frac{8(2k-3)k}{{3+4{k^2}}}$,
同理PB的直线方程为y-3=-k(x-2),可得${x_2}+2=\frac{8k(2k+3)}{{3+4{k^2}}}$,
∴${x_1}+{x_2}=\frac{{16{k^2}-12}}{{3+4{k^2}}},{x_1}-{x_2}=\frac{-48k}{{3+4{k^2}}}$,
∴${k_{AB}}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{{k({x_1}+{x_2})-4k}}{{{x_1}-{x_2}}}$,将${x_1}+{x_2}=\frac{{16{k^2}-12}}{{3+4{k^2}}},{x_1}-{x_2}=\frac{-48k}{{3+4{k^2}}}$代入,化简可求得AB的斜率为$\frac{1}{2}$,是定值.
点评 本题考查椭圆的性质以及抛物线的性质,直线与椭圆的综合问题,解答的关键是认真审题,理清问题与题设的关系,建立合理的方程求出面积函数以及表示出AB的斜率,此类题有一特点即为将直线与椭圆联立,解答中要注意全运会本题中所蕴含的规律.

| x | 1 | 2 | 3 | 4 |
| y | 20 | 30 | 50 | 60 |
(2)若用$\frac{{y}_{i}}{{x}_{i}+3}$(i=1,2,3,4)表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间[0,2)内,则强化训练有效,请问这个班的强化训练是否有效?
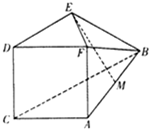 如图,四边形ACDF为正方形,平面ACDF⊥平面BCDE,BC=2DE=2CD=4,DE∥BC,∠CDE=90°,M为AB的中点.
如图,四边形ACDF为正方形,平面ACDF⊥平面BCDE,BC=2DE=2CD=4,DE∥BC,∠CDE=90°,M为AB的中点. 已知AC=BC=$\sqrt{2}$,CD=$\frac{\sqrt{3}}{2}$,AB=BE=EA=2,CD⊥面ABC,面ABE⊥面ABC.
已知AC=BC=$\sqrt{2}$,CD=$\frac{\sqrt{3}}{2}$,AB=BE=EA=2,CD⊥面ABC,面ABE⊥面ABC.