Question

9．如图，四边形ACDF为正方形，平面ACDF⊥平面BCDE，BC=2DE=2CD=4，DE∥BC，∠CDE=90°，M为AB的中点．
（1）证明：EM∥平面ACDF；
（2）求二面角A-BE-C的余弦值．

Answer 1

分析 （1）取AC的中点P，连结PM、PD，通过中位线定理可得四边形DEMP为平行四边形，进而有ME∥DP，利用线面平行的判定定理即得结论；
（2）以C为坐标原点，CA、CB、CD所在直线分别为x、y、z轴建立空间直角坐标系，则所求值为平面ABE的法向量与平面BCE的一个法向量的夹角的余弦值，计算即可．

解答 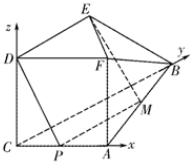（1）证明：如图，取AC的中点P，连结PM、PD，
在△ABC中，P为AC的中点，M为AB的中点，
∴PM∥BC，且PM=$\frac{1}{2}$BC，
又∵DE∥BC，DE=$\frac{1}{2}$BC，∴PM∥DE且PM=DE，
故四边形DEMP为平行四边形，∴ME∥DP，
又∵DP?平面ACDF，EM?平面ACDF，
∴EM∥平面ACDF；
（2）解：∵平面ACDF⊥平面BCDE，平面ACDF∩平面BCDE=CD，AC⊥DC，
∴AC⊥平面BCDE，∴AC⊥BC，
又∵∠CDE=90°，DE∥BC，∴BC⊥CD，
以C为坐标原点，CA、CB、CD所在直线分别为x、y、z轴建立空间直角坐标系，
则C（0，0，0），A（2，0，0），B（0，4，0），D（0，0，2），E（0，2，2），
则$\overrightarrow{AB}$=（-2，4，0），$\overrightarrow{AE}$=（-2，2，2），
设平面ABE的法向量为$\overrightarrow{m}$=（x，y，z），
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AB}=0}\\{\overrightarrow{m}•\overrightarrow{AE}=0}\end{array}\right.$，得$\left\{\begin{array}{l}{-2x+4y=0}\\{-2x+2y+2z=0}\end{array}\right.$，
取y=1，得$\overrightarrow{m}$=（2，1，1），
又∵AC⊥平面BCDE，∴$\overrightarrow{CA}$=（2，0，0）为平面BCE的一个法向量，
∴cos＜$\overrightarrow{m}$，$\overrightarrow{CA}$＞=$\frac{\overrightarrow{m}•\overrightarrow{CA}}{|\overrightarrow{m}||\overrightarrow{CA}|}$=$\frac{2×2}{\sqrt{{2}^{2}+{1}^{2}+{1}^{2}}×2}$=$\frac{\sqrt{6}}{3}$．
∴二面角A-BE-C的余弦值为$\frac{\sqrt{6}}{3}$．

点评 本题考查空间中线面平行的判定，以及求二面角的三角函数值，注意解题方法的积累，属于中档题．