Question

【题目】已知椭圆C： （）的离心率为 ，，，，的面积为1.

（1）求椭圆C的方程；

（2）斜率为2的直线与椭圆交于、两点，求直线的方程；

（3）在轴上是否存在一点，使得过点的任一直线与椭圆若有两个交点、则都有为定值？若存在，求出点的坐标及相应的定值.

Answer 1

【答案】（1）（2）（3）见解析

【解析】

（1）利用离心率和三角形的面积列方程，由此解得的值，进而求得椭圆的方程.（2）设出直线的方程，联立直线的方程和椭圆的方程，根据，斜率乘积为建立方程，解方程求得直线的方程.（3）设出过点的直线方程，联立直线方程和椭圆的方程，消去，化简后写出韦达定理，代入计算，根据为定值，求得点的坐标以及相应的定值.

（1）由已知，，又，解得，

∴椭圆的方程为。

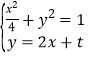（2）设直线的方程为，则由可得，

即

∵∴

∴直线的方程为即。

（3）设、、，当直线不为轴时的方程为，

联立椭圆方程得：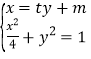

∴当且仅当即时（定值）

即在轴上存在点使得为定值5

点E的坐标为或。经检验，

当直线为轴时上面求出的点也符合题意。