��Ŀ����
����Ŀ����ͼ��ʾ��һ��ˮƽ���õij�������ľ�İ�ȫ���������ĺ��d��ƽ���Ϳ���a�ij˻������ȣ������ij���l��ƽ���ɷ��ȣ� 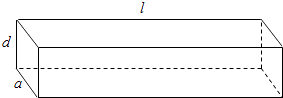
��1����a��d��0�������£�������ľ��ת90�㣨�����ȱ�Ϊ�˺�ȣ�����ľ�İ�ȫ���ɻᷢ���仯�𣿱���DZ�С��
��2������һ�������Ϊ��Բ����Բ�İ뾶ΪR= ![]() ��������ľ�ģ�������ȡ�ɺ����Ϊ�����ε���ľ���䳤�ȼ�Ϊ��ľ�涨�ij���l���ʺ������ν�ȡ����ʹ��ȫ�������
��������ľ�ģ�������ȡ�ɺ����Ϊ�����ε���ľ���䳤�ȼ�Ϊ��ľ�涨�ij���l���ʺ������ν�ȡ����ʹ��ȫ�������
���𰸡�
��1���⣺�谲ȫ����Ϊ ![]()
��ת90��� ![]() ��
��
�ɵã� ![]() ��
��
��a��d��0ʱ�� ![]() ��1
��1
��ʱ��ľ�İ�ȫ���ɱ��
��2���⣺���ȡ�Ŀ�Ϊa��0��a��2 ![]() ������Ϊd��
������Ϊd�� ![]() ����a2+d2=12
����a2+d2=12
�䳤��l��kΪ��ֵ����ȫ����Ϊ ![]()
�� ![]() ��
�� ![]()
��ʱ ![]()
��g�䣨a����0���ɵ� ![]() ��
��
�� ![]()
���Ե���a=2ʱ��g��a��ȡ��ȡ��ֵ����ʱ�� ![]() ��
��
���ԣ�����a=2���� ![]() ʱ����ȫ�������
ʱ����ȫ�������
����������1���谲ȫ����Ϊ ![]() �������ת90���ı���ʽ��Ȼ������ֵ�����ֵ����2�����ȡ�Ŀ�Ϊa��0��a��2
�������ת90���ı���ʽ��Ȼ������ֵ�����ֵ����2�����ȡ�Ŀ�Ϊa��0��a��2 ![]() ������Ϊd��
������Ϊd�� ![]() ���õ���ȫ����Ϊ
���õ���ȫ����Ϊ ![]()
�� ![]() ��
�� ![]() ���ú����ĵ���������ֵ���ɣ�
���ú����ĵ���������ֵ���ɣ�

����Ŀ��ijͶ�ʹ�˾���ṩ����һ����Ͷ�����Ʒ�����һ���Ͷ��ӯ����������±���
Ͷ�ʹ��� | ���� | ���ⲻ | ���� | ������� | ���� | ���ⲻ | ���� | |
���� |
|
|
| ���� |
|
|
|
���ס���������Ͷ�ʹ��ʵĽ����·ֱ�ѡ��Ͷ�ʹ��С��͡�����𡱣���һ���������������һ��ӯ���ĸ��ʴ���![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ��ij������
��ij������![]() ��Ԫ�ʽ𣬾����ڡ�Ͷ�ʹ��С��͡�������������ַ�����ѡ���һ�֣���ôѡ����ַ�����ʹ��һ����Ͷ���������ѧ����ֵ�ϴ�.
��Ԫ�ʽ𣬾����ڡ�Ͷ�ʹ��С��͡�������������ַ�����ѡ���һ�֣���ôѡ����ַ�����ʹ��һ����Ͷ���������ѧ����ֵ�ϴ�.

