题目内容
对于一切实数x不等式ax2+ax-2≤0恒成立,则a的取值范围为( )
| A.(8,0) | B.[-8,0] | C.(8,0] | D.[-8,0) |
当a>0时,显然不能满足对于一切实数x不等式ax2+ax-2≤0恒成立.
当a=0时,对于一切实数x不等式ax2+ax-2≤0恒成立.
当a<0时,∵于一切实数x不等式ax2+ax-2≤0恒成立,∴△=a2+8a≤0,a≠0,
解得-8≤a<0.
综上可得,-8≤a≤0,
故选B.
当a=0时,对于一切实数x不等式ax2+ax-2≤0恒成立.
当a<0时,∵于一切实数x不等式ax2+ax-2≤0恒成立,∴△=a2+8a≤0,a≠0,
解得-8≤a<0.
综上可得,-8≤a≤0,
故选B.

练习册系列答案
相关题目
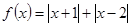 的最小值为
的最小值为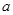 .
.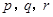 为正实数,且
为正实数,且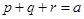 ,求证:
,求证: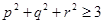 .
.