题目内容
已知0<b<1+a，若关于x的不等式（x－b）2>（ax）2的解集中的整数恰有3个，则（ ）
| A．－1<a<0 | B．0<a<1 | C．1<a<3 | D．3<a<6 |
C
由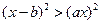
，整理可得（1－
）
－2bx+
>0，由于该不等式的解集中的整数恰有3个，则有1－<0，此时>1，而0<b<1+a，故a>1，
由不等式
<0解得
即
要使该不等式的解集中的整数恰有3个，那么－3<
<－2，由<－2得－b<－2（a－1），则有a<
+1，即a<+1<
+1，解得a<3，由－3<得3a－3>b>0，解得a>1，则1<a<3．
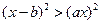，整理可得（1－）－2bx+>0，由于该不等式的解集中的整数恰有3个，则有1－<0，此时>1，而0<b<1+a，故a>1，由不等式
<0解得即要使该不等式的解集中的整数恰有3个，那么－3<<－2，由<－2得－b<－2（a－1），则有a<+1，即a<+1<+1，解得a<3，由－3<得3a－3>b>0，解得a>1，则1<a<3．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
、
、
≥0，且
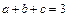，求证
≥
的不等式x2－(a＋1)x＋a＜0
的不等式
在
上恒成立,求实数
的取值范围.
，求
的最小值。
的整数解的集合为{－2}，求实数k的取值范围.
的不等式
对任意
恒成立，则实数
的取值范围是（ ）
