题目内容
1.在某样本的频率分布直方图中,共有7个小长方形,若第三个小长方形的面积为其他6个小长方形的面积和的$\frac{1}{4}$,且样本容量为100,则第三组数据的频数为( )| A. | 25 | B. | 0.2 | C. | 0.25 | D. | 20 |
分析 根据频率分布直方图中频率和为1,列出方程求出第三组的频率与频数即可.
解答 解:根据题意,设第三个小长方形的面积(频率)为x,
则其它6个小长方形的面积和为4x,
∴x+4x=1;
解得x=$\frac{1}{5}$,
∵样本容量为100,
∴第三组的频数为100×$\frac{1}{5}$=20.
故选:D.
点评 本题考查了频率分布直方图的应用问题,解题时利用频率和为1,结合频率=$\frac{频数}{样本容量}$进行解答,是基础题

练习册系列答案
相关题目
9.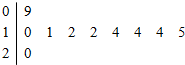 10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )
10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )
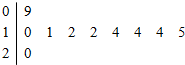 10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )
10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )| A. | 12 | B. | 14 | C. | 15 | D. | 17 |
6.设数列{an}满足a1=0,且2an+1=1+anan+1,bn=$\frac{1}{{\sqrt{n}}}-\sqrt{\frac{{{a_{n+1}}}}{n}}$,记Sn=b1+b2+…+bn,则S100=( )
| A. | $1-\frac{1}{{\sqrt{101}}}$ | B. | $\frac{9}{10}$ | C. | $\frac{99}{100}$ | D. | $\frac{1}{10}-\frac{1}{{\sqrt{101}}}$ |
10.函数f(x)=$\sqrt{x+3}$+$\frac{1}{lg(x+1)}$的定义域是( )
| A. | (-1,0)∪(0,+∞) | B. | [-3,+∞) | C. | [-3,-1)∪(-1,+∞) | D. | (-1,+∞) |
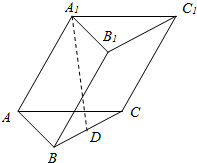 如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.
如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.