题目内容
在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
当箱底边长为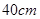 时,箱子容积最大,最大容积是
时,箱子容积最大,最大容积是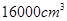 .
.
解析试题分析:设箱底边长为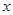
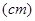 ,则无盖的方底箱子的高
,则无盖的方底箱子的高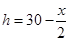
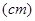 ,其体积为
,其体积为 ,
,
则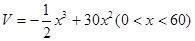
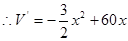 ,
,
令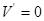 ,得
,得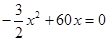 ,解得
,解得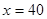 (
( 舍去)
舍去)
当 时,
时,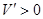 ;当
;当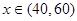 时,
时,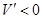 .
.
所以函数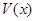 在
在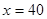 时取得极大值,
时取得极大值,
结合实际情况,这个极大值就是函数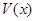 的最大值.
的最大值. 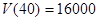 ,
,
故当箱底边长为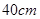 时,箱子容积最大,最大容积是
时,箱子容积最大,最大容积是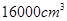 .
.
考点:导数在实际中的运用
点评:解决的关键是合理的设出变量,然后建立空间几何体体积公式,进而得到函数关系式,借助于导数求解最值,易错点是忽略了定义域。属于中档题。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 )万元。
)万元。 百件,生产并销售这种产品得到的利润为当年产量
百件,生产并销售这种产品得到的利润为当年产量 ,求
,求 。
。 上的单调性并加以证明;
上的单调性并加以证明; 的值域是(1,+
的值域是(1,+ ),求a的值。
),求a的值。 ,在
,在 时取得极值.
时取得极值. 的解析式;
的解析式; 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围; ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由. 是定义在
是定义在  上的增函数,且对任意的
上的增函数,且对任意的 都满足
都满足 .
. 的值; (Ⅱ)若
的值; (Ⅱ)若 ,证明
,证明 ;
; ,解不等式
,解不等式  .
.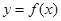 的图象.写出
的图象.写出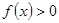 的解集;
的解集;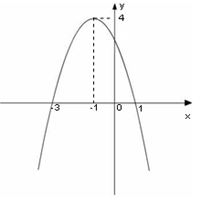
 在何范围内变化时,
在何范围内变化时,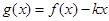 在区间
在区间 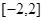 上是单调函数.
上是单调函数. ;
; ,且
,且 ,求
,求 的值。
的值。 ,
,
 时,求
时,求 的最大值和最小值
的最大值和最小值 ,求
,求 的取值范围
的取值范围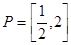 ,函数
,函数 的定义域为
的定义域为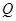
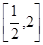 上是增函数,求实数
上是增函数,求实数 的取值范围
的取值范围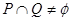 ,求实数
,求实数 的方程
的方程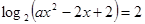 在区间
在区间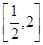 内有解,求实数
内有解,求实数