题目内容
已知函数 ,在
,在 时取得极值.
时取得极值.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(Ⅲ)若 ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
(Ⅰ)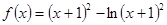 (Ⅱ)
(Ⅱ)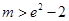 (Ⅲ)
(Ⅲ)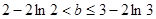
解析试题分析:(Ⅰ)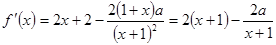 2分
2分
依题意得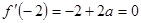 ,所以
,所以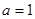 ,从而
,从而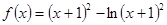 4分
4分
(Ⅱ)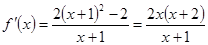 令
令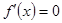 ,得
,得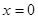 或
或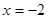 (舍去),
(舍去),
当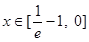 时,
时,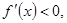 当
当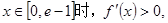
由讨论知 在
在 的极小值为
的极小值为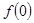 ;最大值为
;最大值为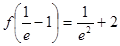 或
或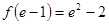 ,因为
,因为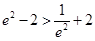 ,所以最大值为
,所以最大值为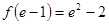 ,所以
,所以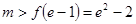 ……8分
……8分
(Ⅲ)设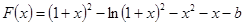 ,即
,即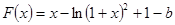 ,
,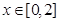 .
.
又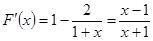 ,令
,令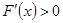 ,得
,得 ;令
;令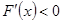 ,得
,得 .
.
所以函数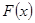 的增区间
的增区间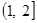 ,减区间
,减区间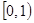 .
.
要使方程有两个相异实根,则有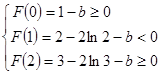 ,解得
,解得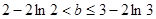 12分
12分
考点:函数导数求函数单调性最值极值
点评:第一问利用函数在极值点处的导数为零得到系数的值,第二问第三问将不等式恒成立问题转化为求函数最值问题,进而利用函数导数求单调性求极值最值。这种转化思路在函数题目中经常用到,要加强这方面的训练

练习册系列答案
相关题目
 ,满足
,满足 ,且方程
,且方程 有两个相等的实根.
有两个相等的实根. 的解析式;
的解析式;
 时,求函数
时,求函数 的表达式.
的表达式. 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层? 平均建筑费用
平均建筑费用 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)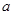 的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?
的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少? 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
) 若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和. (其中
(其中 为大于0的常数),在
为大于0的常数),在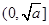 上是减函数,在
上是减函数,在 上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值.
上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值. 
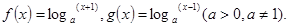 设
设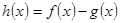
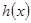 的定义域;
的定义域;