题目内容
3.函数f(x)=lg(x2+100)的值域为[2,+∞).分析 由于y=lgx为增函数,令g(x)=x2+100,则g(x)≥100,由函数的单调性可求得函数y=lg(x2+100)的值域.
解答 解:∵y=lg(x2+100)的底数是10>1,
∴y=lgx为增函数,
令g(x)=x2+100,则g(x)≥100,
∴y=lg(x2+100)≥lg100=2,
∴函数y=lg(x2+100)的值域是[2,+∞).
故答案为:[2,+∞).
点评 本题考查对数函数的值域与最值,熟练掌握y=lgx的性质是解决问题的关键,属于基础题.

练习册系列答案
相关题目
12.不等式|1-3x|≤2的解集为( )
| A. | (-∞,-1] | B. | [-$\frac{1}{3}$,+∞) | C. | [-$\frac{1}{3}$,1] | D. | [-1,$\frac{1}{3}$] |
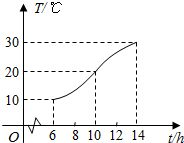 如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中$\frac{π}{2}<φ<π$),与图中曲线对应的函数解析式是$y=10sin(\frac{π}{8}x+\frac{3π}{4})+20,x∈[{6,14}]$.
如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中$\frac{π}{2}<φ<π$),与图中曲线对应的函数解析式是$y=10sin(\frac{π}{8}x+\frac{3π}{4})+20,x∈[{6,14}]$.