题目内容
11.已知函数f(x)=(2cos2x-1)sin2x+$\frac{1}{2}$cos4x.(1)求f(x)的最小正周期及单调减区间;
(2)若α∈(0,π),且f($\frac{α}{4}$-$\frac{π}{8}$)=$\frac{\sqrt{2}}{2}$,求tan(α+$\frac{π}{3}$)的值.
分析 (1)首先,化简函数解析式,然后利用辅助角公式进行化简,然后,根据三角函数的周期公式和单调性进行求解即可;
(2)根据(1),得到f($\frac{α}{4}$-$\frac{π}{8}$)=$\frac{\sqrt{2}}{2}$sin[4($\frac{α}{4}$-$\frac{π}{8}$)+$\frac{π}{4}$],得到相应的α的值,然后,利用两角和的正切公式进行求解即可.
解答 解:(1)∵函数f(x)=(2cos2x-1)sin2x+$\frac{1}{2}$cos4x.
=cos2xsin2x+$\frac{1}{2}$cos4x
=$\frac{1}{2}$sin4x+$\frac{1}{2}$cos4x
=$\frac{\sqrt{2}}{2}$sin(4x+$\frac{π}{4}$),
∴f(x)=$\frac{\sqrt{2}}{2}$sin(4x+$\frac{π}{4}$),
∴T=$\frac{2π}{4}$=$\frac{π}{2}$,
令$\frac{π}{2}$+2kπ≤4x+$\frac{π}{4}$≤$\frac{3π}{2}$+2kπ,k∈Z,
∴$\frac{π}{4}$+2kπ≤4x≤$\frac{5π}{4}$+2kπ,
∴$\frac{π}{16}$+$\frac{kπ}{2}$≤x≤$\frac{5π}{16}$+$\frac{kπ}{2}$,k∈Z,
∴单调减区间[$\frac{π}{16}$+$\frac{kπ}{2}$,$\frac{5π}{16}$+$\frac{kπ}{2}$],(k∈Z),
(2)根据(1),
∵f(x)=$\frac{\sqrt{2}}{2}$sin(4x+$\frac{π}{4}$),
∴f($\frac{α}{4}$-$\frac{π}{8}$)=$\frac{\sqrt{2}}{2}$sin[4($\frac{α}{4}$-$\frac{π}{8}$)+$\frac{π}{4}$]
=$\frac{\sqrt{2}}{2}$sin(α-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,
∴sin(α-$\frac{π}{4}$)=1,
∵α∈(0,π),
∴α-$\frac{π}{4}$∈(-$\frac{π}{4}$,$\frac{3π}{4}$),
∴α-$\frac{π}{4}$=$\frac{π}{2}$,
∴α=$\frac{3π}{4}$,
∴tan(α+$\frac{π}{3}$)=tan($\frac{3π}{4}$+$\frac{π}{3}$)
=$\frac{tan\frac{3π}{4}+tan\frac{π}{3}}{1-tan\frac{3π}{4}tan\frac{π}{3}}$=$\frac{-1+\sqrt{3}}{1-(-1)×\sqrt{3}}$
=$\frac{\sqrt{3}-1}{\sqrt{3}+1}$=2-$\sqrt{3}$.
∴tan(α+$\frac{π}{3}$)的值2-$\sqrt{3}$.
点评 本题重点考查了三角公式、辅助角公式、两角和的正切公式、三角函数的图象与性质等知识,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{13}{23}$ | B. | $\frac{27}{44}$ | C. | $\frac{25}{41}$ | D. | $\frac{23}{38}$ |
| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | $\frac{\sqrt{3}+1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
| A. | 21 | B. | 20 | C. | 19 | D. | 18 |
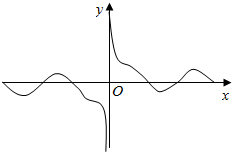 如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g(x)=$\frac{1}{x}$,则Q(x)是( )
如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g(x)=$\frac{1}{x}$,则Q(x)是( )| A. | $\frac{f(x)}{g(x)}$ | B. | f (x)g (x) | C. | f (x)-g(x) | D. | f(x)+g(x) |