题目内容
5.设{an}是公比不为1的等比数列,其前n项和为Sn,若a4,a3,a5成等差数列,则$\frac{S_4}{S_2}$=5.分析 设等比数列{an}的首项为a1,公比为q(q≠1),根据等比数列、等差数列的通项公式得到:2a1q2=a1q3+a1q4,易求q=-2.然后由等比数列的前n项和公式来求所求代数式的值.
解答 解:等比数列{an}的首项为a1,公比为q(q≠1),
∵a4,a3,a5成等差数列,
∴2a3=a4+a5,即2a1q2=a1q3+a1q4,
整理,得(q+2)(q-1)=0,
解得 q=-2或q=1(舍去),
则$\frac{S_4}{S_2}$=$\frac{1-{q}^{4}}{1-{q}^{2}}$=1+q2=1+(-2)2=5.
故答案是:5.
点评 本题考查了等差数列、等比数列的通项公式.熟记公式是解题的关键.

练习册系列答案
相关题目
16.已知函数f(x)=2sin(ωx)(其中常数ω>0),若存在x1∈[-$\frac{2π}{3}$,0],x2∈(0,$\frac{π}{4}$],使f(x1)=f(x2),则ω的取值范围为( )
| A. | ($\frac{3}{2}$,4) | B. | ($\frac{3}{2}$,+∞) | C. | (4,+∞) | D. | (0,$\frac{3}{2}$) |
13.已知函数f(x)=(a-1)x-ax3在[-1,1]的最小值为-1,则实数a的取值范围是( )
| A. | [-1,4] | B. | [-$\frac{1}{2}$,4] | C. | [4,+∞) | D. | [-$\frac{1}{3}$,+∞) |
20.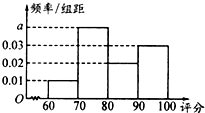 为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测并评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.
为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测并评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.
(I)已知200个合格零件的评分结果的频率分布直方图如图所示.请根据此频率分布直方图,估计这200个零件评分结果的平均数和中位数;
(Ⅱ)根据已有的经验,可能被修复的零件个体被修复的概率如表:
假设每个零件被修复与否相互独立.现有5个零件的评分结果
为(单位:分):38,43,45,52,58,记这5个零件被修复的个数为随机变量X,求X的分布列和数学期望.
 为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测并评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.
为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测并评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.(I)已知200个合格零件的评分结果的频率分布直方图如图所示.请根据此频率分布直方图,估计这200个零件评分结果的平均数和中位数;
(Ⅱ)根据已有的经验,可能被修复的零件个体被修复的概率如表:
| 零件评分结果所在区间 | (40,50] | (50,60] |
| 每个零件个数被修复的概率 | $\frac{1}{3}$ | $\frac{1}{2}$ |
为(单位:分):38,43,45,52,58,记这5个零件被修复的个数为随机变量X,求X的分布列和数学期望.
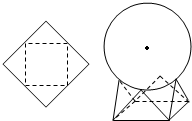 如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将表面积为4π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$.
如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将表面积为4π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$.