题目内容
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() 是半径为
是半径为![]() 的球面上的点,
的球面上的点,![]() ,
,![]() ,点
,点![]() 在
在![]() 上的射影为
上的射影为![]() ,则三棱锥
,则三棱锥![]() 体积的最大值是( )
体积的最大值是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
【解析】如图,
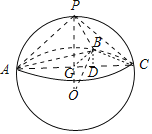
由题意,PA=PB=PC=2,∠ABC=90°,
可知P在平面ABC上的射影G为△ABC的外心,即AC中点,
则球的球心在PG的延长线上,设PG=h,则OG=2﹣h,
∴OB2﹣OG2=PB2﹣PG2,即4﹣(2﹣h)2=4﹣h2,解得h=1.
则AG=CG=![]() ,
,
过B作BD⊥AC于D,设AD=x,则CD=![]() ,
,
再设BD=y,由△BDC∽△ADB,可得![]() ,
,
∴y=![]() ,
, ![]() ,
,
令f(x)=![]() ,则f′(x)=
,则f′(x)=![]()
由f′(x)=0,可得x=![]() ,
,
∴当x=![]() 时,f(x)max=
时,f(x)max=![]() ,
,
∴△ABD面积的最大值为![]() ,
,
则三棱锥P﹣ABD体积的最大值是![]()
故答案为:B.

练习册系列答案
相关题目