Question

【题目】已知函数，.

（1）设，求的最小值；

（2）证明：当时，总存在两条直线与曲线与都相切.

Answer 1

【答案】(1) x＝－1时，F(x)取得最小值F(－1)＝－ (2) 见解析

【解析】试题分析：（1）对函数求导，研究函数的单调性，得到最小值；（2）根据公切线的定义得到(t－1)et－1－t＋a＝0有两个根即可，研究这个函数的单调性和图像，得到这个图像和x轴有两个交点.

解析：

（Ⅰ）F(x)＝(x＋1)ex－1，

当x＜－1时，F(x)＜0，F(x)单调递减；

当x＞－1时，F(x)＞0，F(x)单调递增，

故x＝－1时，F(x)取得最小值F(－1)＝－．

（Ⅱ）因为f(x)＝ex－1，

所以f(x)＝ex－1在点(t，et－1)处的切线为y＝et－1x＋(1－t)et－1；

因为g(x)＝，

所以g(x)＝lnx＋a在点(m，lnm＋a)处的切线为y＝x＋lnm＋a－1，

由题意可得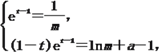则(t－1)et－1－t＋a＝0．

令h(t)＝(t－1)et－1－t＋a，则h(t)＝tet－1－1

由（Ⅰ）得t＜－1时，h(t)单调递减，且h(t)＜0；

当t＞－1时，h(t)单调递增，又h(1)＝0，t＜1时，h(t)＜0，

所以，当t＜1时，h(t)＜0，h(t)单调递减；

当t＞1时，h(t)＞0，h(t)单调递增．

由（Ⅰ）得h(a－1)＝(a－2)ea－2＋1≥－＋1＞0，

又h(3－a)＝(2－a)e2－a＋2a－3＞(2－a)(3－a)＋2a－3＝(a－)2＋＞0，

h(1)＝a－1＜0，所以函数y＝h(t)在(a－1，1)和(1，3－a)内各有一个零点，

故当a＜1时，存在两条直线与曲线f(x)与g(x)都相切．