题目内容
已知圆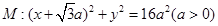 及定点
及定点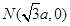 ,点
,点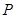 是圆
是圆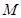 上的动点,点
上的动点,点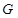 在
在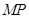 上,且满足
上,且满足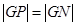 ,
,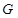 点的轨迹为曲线
点的轨迹为曲线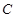 。
。
(1)求曲线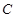 的方程;
的方程;
(2)若点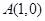 关于直线
关于直线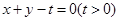 的对称点在曲线
的对称点在曲线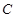 上,求
上,求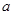 的取值范围。
的取值范围。
(1)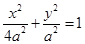 ;(2)
;(2)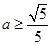 。
。
解析试题分析:(1)本小题首先根据题中的几何条件建立动点与两个定点的距离之和为定值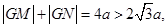 然后结合椭圆的定义可知动点的轨迹为椭圆,并可求得其方程为
然后结合椭圆的定义可知动点的轨迹为椭圆,并可求得其方程为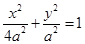 ;
;
(2)本小题首先求得点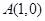 关于直线
关于直线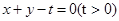 的对称点
的对称点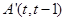 ,再根据点
,再根据点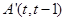 在椭圆
在椭圆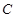 :
: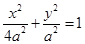 上,则可得
上,则可得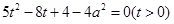 ,然后利用关于
,然后利用关于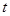
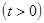 的一元二次方程有正根得到对称轴为
的一元二次方程有正根得到对称轴为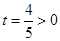 、
、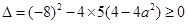 ,解得
,解得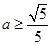 (注意
(注意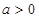 这一条件)
这一条件)
试题解析:(1)设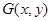 ,
,
∵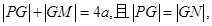
∴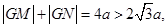
由椭圆定义得:曲线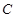 的方程为
的方程为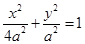 5分
5分
(2)设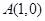 关于直线
关于直线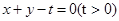 的对称点为
的对称点为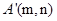 ,则[来源:学§科§网]
,则[来源:学§科§网]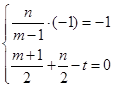 ,∴
,∴ 7分
7分
∴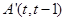 ,
,
∵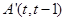 在曲线
在曲线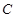 :
: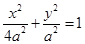 上,
上,
∴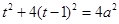 ,
,
化简得: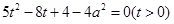 , 9分
, 9分
∵此方程有正根,令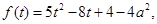 其对称轴为
其对称轴为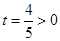 ,
,
∴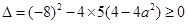 ,
,
∴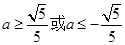 ,
,
∵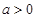 ,∴
,∴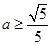 。 12分
。 12分
考点:1 椭圆的定义;2 一元二次方程

练习册系列答案
相关题目
 轴、
轴、 轴上滑动,且
轴上滑动,且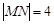 ,点P在线段MN上,满足
,点P在线段MN上,满足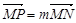
 ,记点P的轨迹为曲线W.
,记点P的轨迹为曲线W.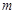 的值的关系;
的值的关系;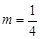 时,设A、B是曲线W与
时,设A、B是曲线W与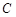 :
: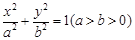 的离心率为
的离心率为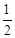 ,右焦点为
,右焦点为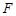 ,右顶点
,右顶点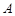 在圆
在圆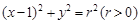 上.
上. 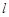 与椭圆
与椭圆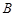 ,与圆
,与圆 .请判断是否存在斜率不为0的直线
.请判断是否存在斜率不为0的直线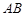 的中点,若存在,求出直线
的中点,若存在,求出直线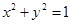 上一个动点,M为点P在y轴上的投影,动点Q满足
上一个动点,M为点P在y轴上的投影,动点Q满足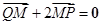 .
.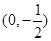 ,交曲线C于A、B两点,且A、B同在以点D(0,1)为圆心的圆上,求直线l的方程。
,交曲线C于A、B两点,且A、B同在以点D(0,1)为圆心的圆上,求直线l的方程。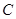 的离心率
的离心率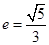 ,一条准线方程为
,一条准线方程为
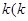 >0)为斜率的直线
>0)为斜率的直线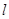 与椭圆
与椭圆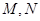 ,且线段
,且线段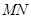 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为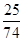 ,求
,求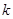 的取值范围。
的取值范围。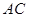 、
、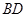 是过抛物线
是过抛物线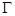 焦点
焦点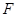 的两条弦,且其焦点
的两条弦,且其焦点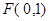 ,
,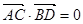 ,点
,点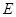 为
为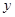 轴上一点,记
轴上一点,记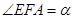 ,其中
,其中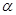 为锐角.
为锐角.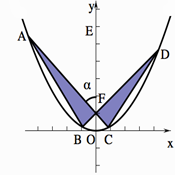
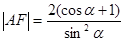 .
.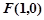 ,点
,点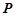 是点
是点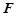 关于
关于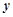 轴的对称点,过点
轴的对称点,过点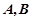 两点。
两点。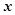 轴上是否存在不同于点
轴上是否存在不同于点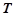 ,使得
,使得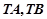 与
与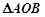 的面积为
的面积为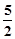 ,求向量
,求向量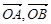 的夹角;
的夹角;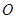 为坐标原点,如果一个椭圆经过点P(3,
为坐标原点,如果一个椭圆经过点P(3,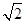 ),且以点F(2,0)为它的一个焦点.
),且以点F(2,0)为它的一个焦点.