题目内容
【题目】已知函数
．
（1）若函数
在
上有三个零点，求实数
的取值范围；
（2）设函数
（
为自然对数的底数），证明：对任意的
，都有
恒成立．
【答案】（1）
（2）见解析
【解析】
试题
(1)利用题意首先讨论函数的单调性，然后结合函数的极值可求得实数
的取值范围为
；
(2)原问题等价于
成立，结合(1)中的结论讨论函数的最值即可证得结论.
试题解析：
解：（1）
，令
，得
，
当
时，
，当
时，
或
，
所以
在
和
上单调递减，在
上单调递增，
所以在
处取得极小值
，在
处取得极大值
，
因为在
上有三个零点，所以有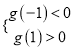
即
，∴
，
即实数的取值范围为；
（2）对任意的
，都有
恒成立，等价于当
时，成立，由（1）知，在
在
上单调递增，在
上单调递减，所以在
上的最大值
，
，令
，得，
因为当
时，
，当时，
，
所以
在上单调递减，在上单调递增，
故的上的最小值
，所以
时，成立.
练习册系列答案
怎样学好牛津英语系列答案
相关题目
【题目】福利彩票“双色球”中红球的号码可以从01，02，03，…，32，33这33个二位号码中选取，小明利用如图所示的随机数表选取红色球的6个号码，选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字，则第四个被选中的红色球号码为（ ）
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16
