题目内容
10.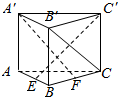 如图直三棱柱ABC-A′B′C′的侧棱长为3,AB⊥BC,且AB=BC=3,点E,F分别是棱AB,BC上的动点,且AE=BF.
如图直三棱柱ABC-A′B′C′的侧棱长为3,AB⊥BC,且AB=BC=3,点E,F分别是棱AB,BC上的动点,且AE=BF.(1)求证:无论E在何处,总有CB′⊥C′E;
(2)当三棱锥B-EB′F的体积取得最大值时,求AE的长度.
(3)在(2)的条件下,求异面直线A′F与AC所成角.
分析 (1)先由线线垂直证明线面垂直,再利用线面垂直的性质证明即可.
(2)利用函数求最值的方法,求解最值时符合的条件,确定E,F是AB,BC的中点,再求解.
(3)根据异面直线所成角的定义进行求解即可.
解答 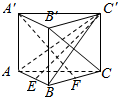 解:(1)连接AC′、BC′,∵BB'C'C是正方形,
解:(1)连接AC′、BC′,∵BB'C'C是正方形,
∴B′C⊥BC′
又∵AB⊥BC,BB′⊥AB,∴AB⊥平面BB′C′C
∴B′C⊥AB,BC′∩AB=B
∴B′C⊥平面ABC′,
又∵C′E?平面ABC′,
∴B′C⊥C′E
(2)设AE=BF=m,∵直三棱柱ABC-A′B′C′,
∴BB′为三棱锥B-EB′F的高,底面△BEF为直角三角形,
∴三棱椎B′-EBF的体积为$V=\frac{1}{2}m(3-m)≤\frac{{{{(m+3-m)}^2}}}{4}=\frac{9}{8}$.
当$m=\frac{3}{2}$时取等号,故当$m=\frac{3}{2}$,
即点E,F分别是棱AB,BC上的中点时,体积最大,
此时△ABC为正三角形,
则AF=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$
(3)由(2)知点E,F分别是棱AB,BC上的中点时,体积最大,
则EF∥AC,
∴∠A′FE为异面直线AC与C′F所成的角;
∵$EF=\frac{{3\sqrt{2}}}{2}$,$AF=A'E=\frac{{3\sqrt{5}}}{2}$,$A'F=\frac{9}{2}$,
∴$|{cos∠A'FE}|=\frac{{\sqrt{2}}}{2}$.
点评 本题考查异面直线所成的以及线面垂直的判定与性质,利用定义法是解决本题的关键.

练习册系列答案
相关题目
1.(理科)在正方体ABCD-A1B1C1D1中,E,F为A1B1,CC1的中点,则异面直线D1E和BF所成角的余弦值为( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{16}{25}$ | D. | -$\frac{16}{25}$ |
18.已知集合U=R,A={x|x2-x-2≥0},则∁UA=( )
| A. | [-1,2] | B. | (-1,2) | C. | (-2,1) | D. | [-2,1) |
5.已知集合A=B={(x,y)|x,y∈R},映射f:A→B,(x,y)→(x+y,x-y),则在映射f下,象(2,1)的原象是( )
| A. | ($\frac{3}{2}$,-$\frac{1}{2}$) | B. | ($\frac{3}{2}$,$\frac{1}{2}$) | C. | (3,1) | D. | (1,3) |
2.函数f(x)=$sin({2x+\frac{π}{6}})$的最小正周期和振幅分别是( )
| A. | π,1 | B. | π,2 | C. | 2π,1 | D. | 2π,2 |
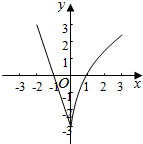 函数f(x)=$\left\{\begin{array}{l}{ax+b(x≤0)}\\{lo{g}_{e}(x+\frac{1}{8})(x>0)}\end{array}\right.$的图象如图所示.
函数f(x)=$\left\{\begin{array}{l}{ax+b(x≤0)}\\{lo{g}_{e}(x+\frac{1}{8})(x>0)}\end{array}\right.$的图象如图所示.