题目内容
15.设集合A={-1,0,1,2,3},B={x|x2-2x>0},则A∩B={-1,3}.分析 求出B中不等式的解集确定出B,找出A与B的交集即可.
解答 解:由B中不等式变形得:x(x-2)>0,
解得:x<0或x>2,即B={x|x<0或x>2},
∵A={-1,0,1,2,3},
∴A∩B={-1,3},
故答案为:{-1,3}
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7.计算$\frac{\sqrt{x}•\root{3}{{x}^{4}}}{x•\root{6}{x}}$的值为( )
| A. | ${x}^{\frac{2}{3}}$ | B. | ${x}^{-\frac{2}{3}}$ | C. | ${x}^{\frac{1}{3}}$ | D. | ${x}^{-\frac{1}{3}}$ |
5.已知函数f(x)=$\left\{{\begin{array}{l}{(1-3a)x+10a,x≤7}\\{{a^{x-7}},x>7}\end{array}}$是定义域(-∞,+∞)上的单调递减函数,则实数a的取值范围是( )
| A. | $(\frac{1}{3},\frac{1}{2})$ | B. | ($\frac{1}{3}$,$\frac{6}{11}$] | C. | $[\frac{1}{2},\frac{2}{3})$ | D. | $(\frac{1}{2},\frac{6}{11}]$ |
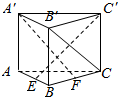 如图直三棱柱ABC-A′B′C′的侧棱长为3,AB⊥BC,且AB=BC=3,点E,F分别是棱AB,BC上的动点,且AE=BF.
如图直三棱柱ABC-A′B′C′的侧棱长为3,AB⊥BC,且AB=BC=3,点E,F分别是棱AB,BC上的动点,且AE=BF.