题目内容
18.已知集合U=R,A={x|x2-x-2≥0},则∁UA=( )| A. | [-1,2] | B. | (-1,2) | C. | (-2,1) | D. | [-2,1) |
分析 求出A中不等式的解集确定出A,根据全集U=R,求出A的补集即可.
解答 解:由A中不等式变形得:(x-2)(x+1)≥0,
解得:x≤-1或x≥2,即A=(-∞,-1]∪[2,+∞),
∵U=R,
∴∁UA=(-1,2),
故选:B.
点评 此题考查了补集及其运算,熟练掌握补集的定义是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
9.函数f(x)=$\frac{1}{\sqrt{a{x}^{2}+3ax+1}}$的定义域是R,则实数a的取值范围是( )
| A. | $({0,\frac{4}{9}})$ | B. | $[{0,\frac{4}{9}}]$ | C. | $[{0,\frac{4}{9}})$ | D. | $({0,\frac{4}{9}}]$ |
13.连锁经营公司所属5个零售店某月的销售额利润资料如表:
(1)画出销售额和利润额的散点图
(2)若销售额和利润额具有相关关系,试计算利润额y对销售额x的回归直线方程.
(3)估计要达到1000万元的利润额,销售额约为多少万元.
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$x)
| 商品名称 | A | B | C | D | E |
| 销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
| 利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(2)若销售额和利润额具有相关关系,试计算利润额y对销售额x的回归直线方程.
(3)估计要达到1000万元的利润额,销售额约为多少万元.
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$x)
7.计算$\frac{\sqrt{x}•\root{3}{{x}^{4}}}{x•\root{6}{x}}$的值为( )
| A. | ${x}^{\frac{2}{3}}$ | B. | ${x}^{-\frac{2}{3}}$ | C. | ${x}^{\frac{1}{3}}$ | D. | ${x}^{-\frac{1}{3}}$ |
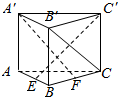 如图直三棱柱ABC-A′B′C′的侧棱长为3,AB⊥BC,且AB=BC=3,点E,F分别是棱AB,BC上的动点,且AE=BF.
如图直三棱柱ABC-A′B′C′的侧棱长为3,AB⊥BC,且AB=BC=3,点E,F分别是棱AB,BC上的动点,且AE=BF.