题目内容
4.设f(x)=3x,g(x)=($\frac{1}{3}$)x.(1)在同一坐标系中作出f(x),g(x)的图象.
(2)计算f(1)与g(-1),f(π)与g(-π),f(m)与g(-m)的值,从中你能得到什么结论?
分析 (1)结合指数函数的图象,利用描点法作f(x),g(x)的图象.
(2)可求得f(1)=3,g(-1)=3;f(π)=3π,g(-π)=3π;f(m)=3m,g(-m)=3m;从而可判断f(x)=g(-x).
解答 解:(1)作f(x),g(x)的图象如下,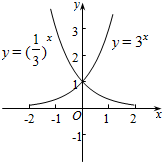 ,
,
(2)f(1)=3,g(-1)=3;
f(π)=3π,g(-π)=3π;
f(m)=3m,g(-m)=3m;
故f(x)=g(-x);
即f(x)与g(x)的图象关于y轴对称.
点评 本题考查了指数函数的图象的作法及由图象发现函数的性质的方法应用.

练习册系列答案
相关题目
9.函数f(x)=$\frac{1}{\sqrt{a{x}^{2}+3ax+1}}$的定义域是R,则实数a的取值范围是( )
| A. | $({0,\frac{4}{9}})$ | B. | $[{0,\frac{4}{9}}]$ | C. | $[{0,\frac{4}{9}})$ | D. | $({0,\frac{4}{9}}]$ |
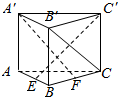 如图直三棱柱ABC-A′B′C′的侧棱长为3,AB⊥BC,且AB=BC=3,点E,F分别是棱AB,BC上的动点,且AE=BF.
如图直三棱柱ABC-A′B′C′的侧棱长为3,AB⊥BC,且AB=BC=3,点E,F分别是棱AB,BC上的动点,且AE=BF.