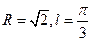题目内容
如图,在四棱锥P-ABCD中,底面ABCD为正方形,且边长为2a,棱PD⊥底面ABCD,PD=2b,取各侧棱的中点E,F,G,H,写出点E,F,G,H的坐标.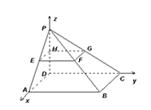

E(a,0,b),F(a,a,b),G(0,a,b),H(0,0,b)
由图形知,DA⊥DC,DC⊥DP,DP⊥DA,故以D为原点,建立如图空间坐标系D-xyz.
因为E,F,G,H分别为侧棱中点,由立体几何知识可知,平面EFGH与底面ABCD平行,
从而这4个点的竖坐标都为P的竖坐标的一半,也就是b,
由H为DP中点,得H(0,0,b)
E在底面面上的投影为AD中点,所以E的横坐标和纵坐标分别为a和0,所以E(a,0,b),
同理G(0,a,b);F在坐标平面xOz和yOz上的投影分别为点E和G,故F与E横坐标相同都是a,
与G的纵坐标也同为a,又F竖坐标为b,故F(a,a,b).
因为E,F,G,H分别为侧棱中点,由立体几何知识可知,平面EFGH与底面ABCD平行,
从而这4个点的竖坐标都为P的竖坐标的一半,也就是b,
由H为DP中点,得H(0,0,b)
E在底面面上的投影为AD中点,所以E的横坐标和纵坐标分别为a和0,所以E(a,0,b),
同理G(0,a,b);F在坐标平面xOz和yOz上的投影分别为点E和G,故F与E横坐标相同都是a,
与G的纵坐标也同为a,又F竖坐标为b,故F(a,a,b).

练习册系列答案
相关题目
 = a,
= a, = b,
= b, = c,G∈平面ABC.则G为△ABC的重心的充分必要条件是
= c,G∈平面ABC.则G为△ABC的重心的充分必要条件是 (a+b+c);
(a+b+c);
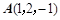 关于面
关于面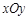 的对称点为
的对称点为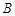 ,而
,而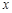 轴的对称点为
轴的对称点为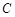 ,则
,则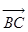 = ( )
= ( )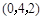
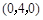
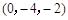
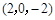
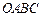 中,
中,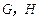 分别是
分别是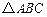 ,
,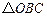 的重心,设
的重心,设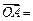
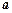 ,
,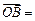
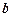 ,
,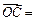
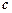 ,试用向量
,试用向量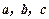 表示向量
表示向量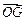 和
和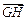 .
.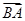 =(2,3),
=(2,3),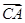 =(4,7),则
=(4,7),则 =( )
=( ) 、
、 ,则该球的半径R及点A、B在该球面上的最短距离
,则该球的半径R及点A、B在该球面上的最短距离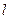 分别为
分别为 B.
B.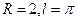 C.
C. D.
D.