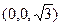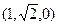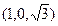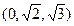题目内容
已知在四面体ABCD中, = a,
= a, = b,
= b, = c,G∈平面ABC.则G为△ABC的重心的充分必要条件是
= c,G∈平面ABC.则G为△ABC的重心的充分必要条件是 (a+b+c);
(a+b+c);
 = a,
= a, = b,
= b, = c,G∈平面ABC.则G为△ABC的重心的充分必要条件是
= c,G∈平面ABC.则G为△ABC的重心的充分必要条件是 (a+b+c);
(a+b+c);
证明见解析
证明:必要性:连AG交BC于D,则D平分BC,且G分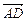 所成的比为2∶1,从而
所成的比为2∶1,从而
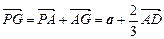 ,
,
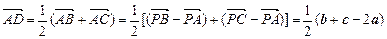 ,
,
故 .
.
充分性:设D分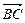 所成的比为p,G分
所成的比为p,G分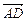 所成的比为q.
所成的比为q.
则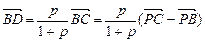 ,
, 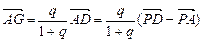
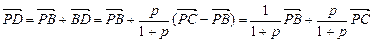 ,
,
于是,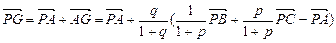
=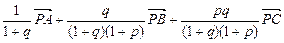
因 (a+b+c),故
(a+b+c),故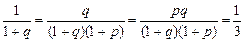 ,
,
解得q =2,p = 1,于是G为△ABC的重心.
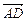 所成的比为2∶1,从而
所成的比为2∶1,从而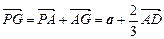 ,
,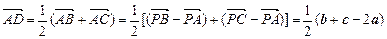 ,
,故
 .
.充分性:设D分
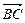 所成的比为p,G分
所成的比为p,G分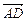 所成的比为q.
所成的比为q.则
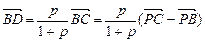 ,
, 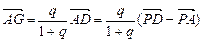
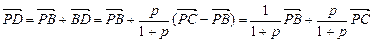 ,
,于是,
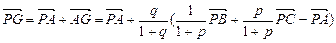
=
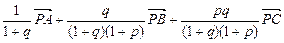
因
 (a+b+c),故
(a+b+c),故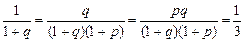 ,
,解得q =2,p = 1,于是G为△ABC的重心.

练习册系列答案
相关题目
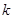 a+b与2 a-b互相垂直,则
a+b与2 a-b互相垂直,则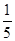
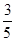
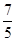
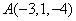 ,则点
,则点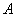 关于
关于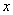 轴对称的点的坐标为( )
轴对称的点的坐标为( )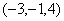
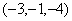
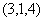
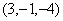
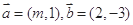 ,若满足
,若满足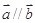 ,则
,则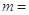 .
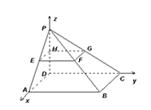
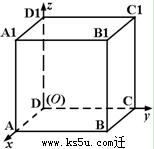
.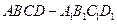 的顶点D为坐标原点O,如图建立空间直角坐标系,则与
的顶点D为坐标原点O,如图建立空间直角坐标系,则与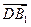 共线的向量的坐标可以是
共线的向量的坐标可以是
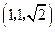
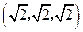
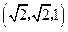
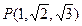 作
作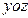 平面的垂线
平面的垂线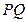 ,则垂足
,则垂足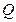 的坐标是( ).
的坐标是( ).