题目内容
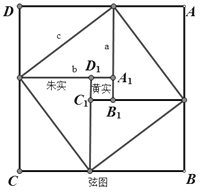
【题目】部分与整体以某种相似的方式呈现称为分形，一个数学意义上分形的生成是基于一个不断迭代的方程式，即一种基于递归的反馈系统，分形几何学不仅让人们感悟到科学与艺术的融合，数学与艺术审美的统一，而且还有其深刻的科学方法论意义，如图，由波兰数学家谢尔宾斯基1915年提出的谢尔宾斯基三角形就属于一种分形，具体作法是取一个实心三角形，沿三角形的三边中点连线.将它分成4个小三角形，去掉中间的那一个小三角形后，对其余3个小三角形重复上述过程逐次得到各个图形，若记图①三角形的面积为
，则第n个图中阴影部分的面积为（ ）
A.
B.
C.
D.
【答案】D
【解析】
每一个图形的面积是前一个图形面积的
，根据等比数列公式得到答案.
根据题意：每一个图形的面积是前一个图形面积的，即面积为首项为
，公比为的等比数列，
故第n个图中阴影部分的面积为
.
故选：D.
课课优能力培优100分系列答案
优百分课时互动系列答案【题目】为了调查某地区70岁以上老人是否需要志愿者提供帮助，用简单随机抽样的方法从该地区调查了100位70岁以上老人，结果如下：
男 | 女 | |
需要 | 18 | 5 |
不需要 | 32 | 45 |
（1）估计该地区70岁以上老人中，男、女需要志愿者提供帮助的比例各是多少？
（2）能否有
的把握认为该地区70岁以上的老人是否需要志愿者提供帮助与性别有关；
（3）根据（2）的结论，能否提供更好的调查方法来估计该地区70岁以上老人中，需要志愿者提供帮助的老人的比例？说明理由.
附：
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
，
.
【题目】新冠状病毒严重威胁着人们的身体健康，我国某医疗机构为了调查新冠状病毒对我国公民的感染程度，选了某小区的
位居民调查结果统计如下：
感染 | 不感染 | 合计 | |
年龄不大于 |
| ||
年龄大于 |
| ||
合计 |
|
|
（1）根据已知数据，把表格数据填写完整；
（2）能否在犯错误的概率不超过
的前提下认为感染新冠状病与不同年龄有关？
（3）已知在被调查的年龄大于
岁的感染者中有
名女性，其中
位是女教师，现从这名女性中随机抽取
人，求至多有
位教师的概率．
附：
，
.
|
|
|
|
|
|
|
|
|
|
【题目】为了研究“教学方式”对教学质量的影响，某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学（勤奋程度和自觉性都一样）.以下茎叶图为甲、乙两班（每班均为20人）学生的数学期末考试成绩．
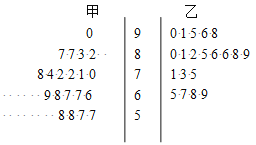
（1）学校规定：成绩不低于75分的为优秀．请画出下面的
列联表．
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
（2）判断有多大把握认为“成绩优秀与教学方式有关”．
下面临界值表仅供参考：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式： 
【题目】A、B两种品牌各三种车型2017年7月的销量环比(与2017年6月比较)增长率如下表：
A品牌车型 | A1 | A2 | A3 | ||||
环比增长率 | -7.29% | 10.47% | 14.70% | ||||
B品牌车型 | B1 | B2 | B3 | ||||
环比增长率 | -8.49% | -28.06% | 13.25% | ||||
根据此表中的数据，有如下关于7月份销量的四个结论:①A1车型销量比B1车型销量多；
②A品牌三种车型总销量环比增长率可能大于14.70%；
③B品牌三款车型总销量环比增长率可能为正；
④A品牌三种车型总销量环比增长率可能小于B品牌三种车型总销量环比增长率．
其中正确结论的个数是( )
A. 
B. 
C. 
D. 
