题目内容
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形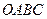 中,已知过点
中,已知过点 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若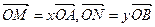 。
。
(1)求证: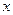 与
与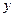 的关系为
的关系为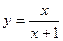 ;
;
(2)设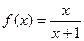 ,定义函数
,定义函数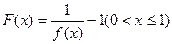 ,点列
,点列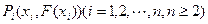 在函数
在函数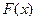 的图像上,且数列
的图像上,且数列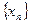 是以首项为1,公比为
是以首项为1,公比为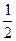 的等比数列,
的等比数列,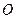 为原点,令
为原点,令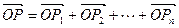 ,是否存在点
,是否存在点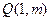
 ,使得
,使得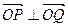 ?若存在,请求出
?若存在,请求出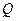 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数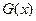 为
为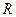 上偶函数,当
上偶函数,当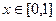 时
时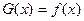 ,又函数
,又函数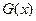 图象关于直线
图象关于直线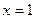 对称,当方程
对称,当方程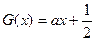 在
在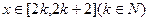 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数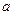 的取值范围。
的取值范围。
在平行四边形
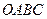 中,已知过点
中,已知过点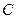 的直线与线段
的直线与线段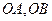 分别相交于点
分别相交于点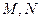 。若
。若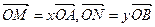 。
。(1)求证:
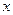 与
与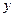 的关系为
的关系为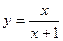 ;
;(2)设
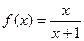 ,定义函数
,定义函数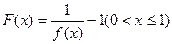 ,点列
,点列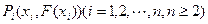 在函数
在函数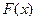 的图像上,且数列
的图像上,且数列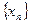 是以首项为1,公比为
是以首项为1,公比为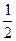 的等比数列,
的等比数列,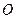 为原点,令
为原点,令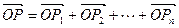 ,是否存在点
,是否存在点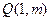
 ,使得
,使得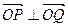 ?若存在,请求出
?若存在,请求出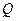 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。(3)设函数
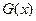 为
为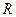 上偶函数,当
上偶函数,当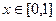 时
时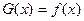 ,又函数
,又函数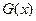 图象关于直线
图象关于直线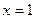 对称,当方程
对称,当方程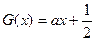 在
在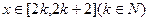 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数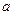 的取值范围。
的取值范围。略
(1) ,…………………………………………2分
,…………………………………………2分
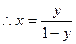 ,从而
,从而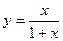 。…………………………………………………4分
。…………………………………………………4分
(2)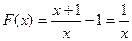 ,
,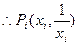 ,又
,又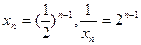 ,
,
…………………………………………………………6分
 。
。
…………………………………………………………8分
设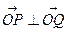 ,则
,则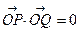 。
。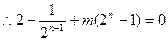 ,
,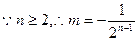 ,
,
故存在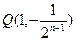 满足条件。…………………………………………………10分
满足条件。…………………………………………………10分
(3)当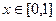 时,
时,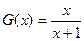 ,又由条件得
,又由条件得
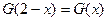 ,
,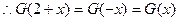 。
。
当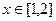 时,
时,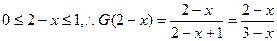 ,
,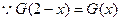 ,
,
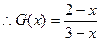 ,从而
,从而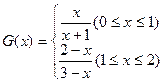 。…………………12分
。…………………12分
由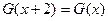 得
得
 。……………
。…………… ……………14分
……………14分
设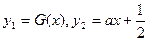 ,在同一直角坐标系中作出两函数的图
,在同一直角坐标系中作出两函数的图 像,如图
像,如图
当函数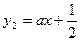 图像经过点
图像经过点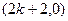 时,
时,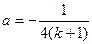 。
。
…………………………………………………………16分
由图像可知,当
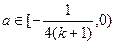 时,
时,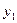 与
与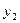 的图像在
的图像在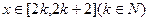 有两个不同交点,因此方程
有两个不同交点,因此方程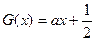 在
在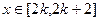 上有两个不同的解。
上有两个不同的解。
…………………………………………………………18分
 ,…………………………………………2分
,…………………………………………2分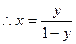 ,从而
,从而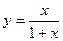 。…………………………………………………4分
。…………………………………………………4分(2)
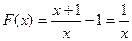 ,
,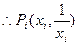 ,又
,又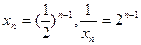 ,
,…………………………………………………………6分
 。
。…………………………………………………………8分
设
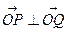 ,则
,则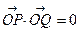 。
。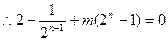 ,
,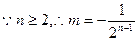 ,
,故存在
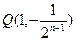 满足条件。…………………………………………………10分
满足条件。…………………………………………………10分(3)当
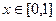 时,
时,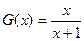 ,又由条件得
,又由条件得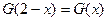 ,
,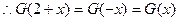 。
。当
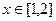 时,
时,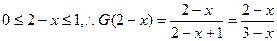 ,
,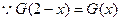 ,
,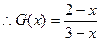 ,从而
,从而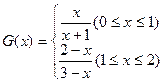 。…………………12分
。…………………12分由
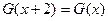 得
得 。……………
。…………… ……………14分
……………14分设
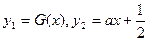 ,在同一直角坐标系中作出两函数的图
,在同一直角坐标系中作出两函数的图 像,如图
像,如图当函数
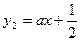 图像经过点
图像经过点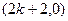 时,
时,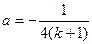 。
。…………………………………………………………16分
由图像可知,当

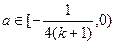 时,
时,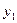 与
与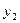 的图像在
的图像在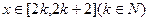 有两个不同交点,因此方程
有两个不同交点,因此方程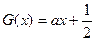 在
在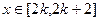 上有两个不同的解。
上有两个不同的解。…………………………………………………………18分

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 1和
1和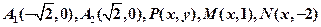 ,若实数
,若实数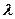 使得
使得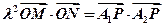 (
(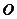 为坐标原点)
为坐标原点)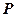 点的轨迹方程,并讨论
点的轨迹方程,并讨论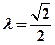 时,若过点
时,若过点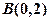 的直线
的直线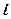 与(1)中
与(1)中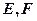 (
(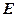 在
在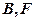 之间),试求
之间),试求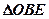 与
与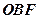 面积之比的取值范围。
面积之比的取值范围。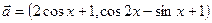 ,
,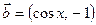 ,定义
,定义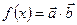
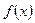 的
的 最小正周期和单调递减区间;
最小正周期和单调递减区间;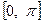 上的最大值及取得最大值时的
上的最大值及取得最大值时的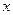 。
。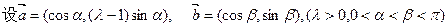 是平面上的两个向量,且
是平面上的两个向量,且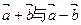 互为垂直. (1)求
互为垂直. (1)求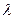 的值; (2)若
的值; (2)若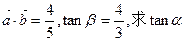 的值.
的值.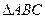 中,角A,B,C对应边分别是a,b,c,
中,角A,B,C对应边分别是a,b,c,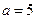 ,
,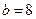 ,
,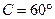 ,则
,则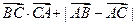 等于( )
等于( )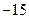
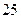
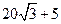
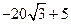
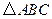 中,
中,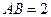 ,
,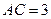 ,
,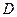 是边
是边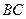 的中点,则
的中点,则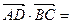 ;
;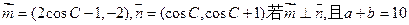 ,则△ABC周长的最小值为 ( )
,则△ABC周长的最小值为 ( )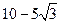
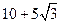
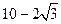

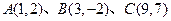 ,若
,若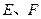 为线段
为线段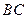 的三等分点,则
的三等分点,则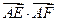 = 。
= 。