题目内容
【题目】如图，已知圆C的圆心在直线l：y=2x﹣4上，半径为1，点A（0，3）． （Ⅰ）若圆心C也在直线y=x﹣1上，过点A作圆C的切线，求切线的方程；
（Ⅱ）若圆C上存在点M，使|MA|=2|MO|（O为坐标原点），求圆心C的横坐标a的取值范围．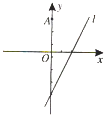
【答案】解：（Ⅰ）由 
，得圆心C（3，2），过点A作圆C的切线斜率存在，设A点的圆C的切线的方程：y=kx+3，即kx﹣y+3=0．由题意， 
，解得k=0，k= 
，所求切线方程为：y=3或3x+4y﹣12=0； （Ⅱ）∵圆C的圆心在直线l：y=2x﹣4上，
∴圆C的方程设为：（x﹣a）2+（y﹣（2a﹣4））2=1，设M（x，y），由|MA|=2|MO|，可得： 
，化简可得x2+（y+1）2=4，点M在以D（0，﹣1）为圆心，2为半径的圆上．
由题意，点M（x，y）在圆上，
∴圆C和圆D有公共点，则|2﹣1|≤|CD|≤2+1，
∴1 
≤3，即1 
，5a2﹣12a+8≥0，可得a∈R，由5a2﹣12a≤0，可得0 
，
圆心C的横坐标a的取值范围： 
【解析】（Ⅰ）求出圆心C的坐标，设出点A作圆C的切线方程，利用点到直线的距离等于半径，然后求切线的方程；（Ⅱ）设出圆C的方程，点M的坐标，利用|MA|=2|MO|，求出M的轨迹，通过两个圆的位置关系，求圆心C的横坐标a的取值范围．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
