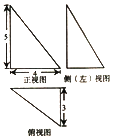
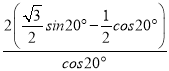��Ŀ����
����Ŀ������![]() ����СֵΪ
����СֵΪ![]() .
.
��1����![]() ��
��
��2����![]() ����
����![]() ����ʱ
����ʱ![]() �����ֵ.
�����ֵ.
���𰸡�(1) 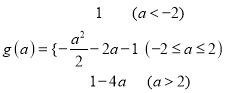 ��(2)�𰸼�����.
��(2)�𰸼�����.
�������������������1������ͬ�����Ǻ�����Ļ�����ϵ����������ʽ�������������![]() С�ک�1ʱ��
С�ک�1ʱ��![]() ���ک�1��С��1ʱ��
���ک�1��С��1ʱ��![]() ����1ʱ�����ݶ��κ�������Сֵ�ķ������f��x������Сֵg��a����ֵ���ɣ���2����
����1ʱ�����ݶ��κ�������Сֵ�ķ������f��x������Сֵg��a����ֵ���ɣ���2����![]() ���뵽��һ�ʵ�g��a���ĵڶ��͵���������ʽ�У����a��ֵ������f��x���еõ�f��x���Ľ���ʽ�������䷽�ɵ�f��x�������ֵ��
���뵽��һ�ʵ�g��a���ĵڶ��͵���������ʽ�У����a��ֵ������f��x���еõ�f��x���Ľ���ʽ�������䷽�ɵ�f��x�������ֵ��
���������
��1����![]()
![]() .����
.����![]()
����![]() ��
��![]() ʱ��
ʱ�� ![]()
����![]() ��
��![]() ʱ��
ʱ�� ![]()
����![]() ��
��![]() ʱ��
ʱ�� ![]()
���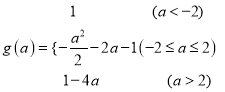
��2��![]()
![]() ����
����![]() ������
������![]() ��
��![]() ��ì�ܣ�
��ì�ܣ�
����![]() ������
������![]() ��
��![]() ��
��![]() ���ᣩ.
���ᣩ.
![]()
![]() ʱ��
ʱ�� ![]() ��ʱ
��ʱ![]()
��![]() ʱ��
ʱ�� ![]() ȡ�����ֵΪ5.
ȡ�����ֵΪ5.
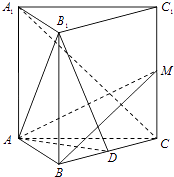
�㾦�����κ����ڱ������ϱ������ֵ����Сֵ����ֻ��������Ķ˵����κ���ͼ��Ķ��㴦ȡ�������������У���1����̶�����Ҳ�̶�����2���ᶯ���Ậ������������̶�����3����̶������䶯�����京������. ����ֵ�Ĺؼ��ǣ���1��ͼ��Ŀ��ڷ���2���Գ����������λ�ù�ϵ����3�����ͼ������ȷ��������ֵ.
�����͡������
��������
21
����Ŀ����֪���������ߵ�����![]() �ļн�Ϊ
�ļн�Ϊ![]() ����
����![]() Ϊ��ʵ��.
Ϊ��ʵ��.
��1����![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��
��2����![]() ����
����![]() ����Сֵ����Ӧ��
����Сֵ����Ӧ��![]() ��ֵ����ָ����ʱ����
��ֵ����ָ����ʱ����![]() ��
��![]() ��λ�ù�ϵ.
��λ�ù�ϵ.
��3����![]() Ϊ��ǣ�������ʵ��
Ϊ��ǣ�������ʵ��![]() ������
������![]() �ķ���
�ķ���![]() ��������ͬ����ʵ���⣬��
��������ͬ����ʵ���⣬��![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
���𰸡�(1) ![]() ��(2)�𰸼�������(3)
��(2)�𰸼�������(3) ![]() .
.
�������������������1������![]() +2
+2![]() ��
��![]() ��4
��4![]() ��ֱ����
��ֱ���� ![]() +2
+2![]() ����
����![]() ��4
��4![]() ��=0���ɵã����������tan�ȣ�
��=0���ɵã����������tan�ȣ�
��2�����ö��κ��������ʣ�����|x![]() ��
��![]() |����Сֵ����Ӧ��x��ֵ��������������ʽ����ȷ������
|����Сֵ����Ӧ��x��ֵ��������������ʽ����ȷ������![]() ��x
��x![]() ��
��![]() ��λ�ù�ϵ��
��λ�ù�ϵ��
��3������|x![]() ��
��![]() |=|m
|=|m![]() |���ȼ���9x2��3cos��x+1��9m2=0�����ù���x�ķ���|x
|���ȼ���9x2��3cos��x+1��9m2=0�����ù���x�ķ���|x![]() ��
��![]() |=|m
|=|m![]() |��������ͬ����ʵ���⣬��������ʽ������ȷ�����ۣ�
|��������ͬ����ʵ���⣬��������ʽ������ȷ�����ۣ�
���������
��1�������⣬��![]() ��
��![]()
![]() ��
��![]() ��
��![]() ����
����![]()
��ˣ� 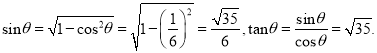
��2��![]()
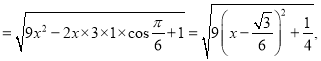 �ʵ�
�ʵ�![]() ʱ��
ʱ�� ![]() ȡ����СֵΪ
ȡ����СֵΪ![]() ��ʱ��
��ʱ�� ![]()
������![]() ��
��![]() ��ֱ.
��ֱ.
��3���Է���![]() ����ƽ������
����ƽ������![]() ��
��
�跽�̢ٵ�������ͬ��ʵ����Ϊ![]() ���������⣬��
���������⣬��
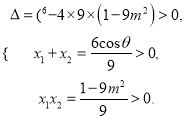 ��
��
��֮����![]()
��![]() �̢ٿ��Ի�Ϊ
�̢ٿ��Ի�Ϊ![]() ��
��
��![]() ��
��![]() ����֪
����֪![]() ��
��![]()
��![]() ����
����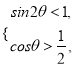 ����
����![]() ����
����![]() .
.
��![]() ����
����![]() ʱ��
ʱ�� ![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]() ����
����![]() }��
}��
��![]() ����
����![]() ʱ��
ʱ�� ![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]() .
.