题目内容
【题目】已知中心在坐标原点O,焦点在x轴上,离心率为![]() 的椭圆过点
的椭圆过点![]() .
.
(1)求椭圆的方程;
(2)设不过原点O的直线l与该椭圆交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,若![]() 的面积为
的面积为![]() ,求直线l与y轴交点的坐标.
,求直线l与y轴交点的坐标.
【答案】(1)![]() ;(2)
;(2)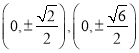
【解析】
(1)设出椭圆的方程,将已知点代入椭圆的方程及利用椭圆的离心率公式得到关于椭圆的三个参数的等式,解方程组求出![]() 的值,代入椭圆方程即可.(2)设出直线的方程将直线方程与椭圆方程联立,消去
的值,代入椭圆方程即可.(2)设出直线的方程将直线方程与椭圆方程联立,消去![]() 得到关于
得到关于![]() 的二次方程,利用韦达定理得到关于两个交点的坐标的关系,将直线
的二次方程,利用韦达定理得到关于两个交点的坐标的关系,将直线![]() 的斜率用坐标表示据已知三个斜率成等比数列,列出方程,将韦达定理得到的等式代入,求出
的斜率用坐标表示据已知三个斜率成等比数列,列出方程,将韦达定理得到的等式代入,求出![]() 的值,利用判别式大于
的值,利用判别式大于![]() 得到
得到![]() 的范围,将
的范围,将![]() 面积表示出来,得到
面积表示出来,得到![]() 的等式,解出
的等式,解出![]() ,即可得到直线l与y轴交点的坐标.
,即可得到直线l与y轴交点的坐标.
(1)设椭圆方程为:![]() ,
,
椭圆的离心率为![]() ,过点
,过点![]() ,
,
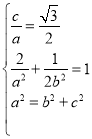 ,解得
,解得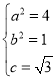 ,
,
![]() 椭圆的方程为:
椭圆的方程为:![]() .
.
(2)由题意知,直线![]() 的斜率存在且不为0,
的斜率存在且不为0,
设直线![]() 的方程为:
的方程为:![]() ,
,
![]()
![]() ,消
,消![]() 得,
得,![]() ,
,
![]()
且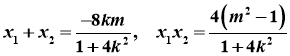 ,
,
![]() ,
,
![]() 直线
直线![]() 的斜率依次成等比数列,
的斜率依次成等比数列,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,即
,即![]() ,
,
![]() 直线
直线![]() 的斜率存在,且
的斜率存在,且![]() ,得
,得![]() 且
且![]() .
.
设![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离,
![]()
![]()
![]()
![]() 或
或![]() ,
,
![]() 直线
直线![]() 与
与![]() 轴交点的坐标为:
轴交点的坐标为: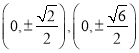 .
.

【题目】某市食品药品监督管理局开展2020年春季快递餐饮安全检查,对本市的8个快递配餐点进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如表所示:
快递配餐点编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分 | 82 | 75 | 70 | 66 | 83 | 93 | 95 | 100 |
卫生标准评分 | 81 | 79 | 77 | 75 | 82 | 83 | 84 | 87 |
(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(精确到0.1)
的线性回归方程;(精确到0.1)
(2)现从8个被检查点中任意抽取两个组成一组,若两个点的原料采购加工标准和卫生标准的评分均超过80分,则组成“快递标兵配餐点”,求该组被评为“快递标兵配餐点”的概率.
参考公式: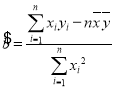 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.


