题目内容
【题目】如图所示，M、N、P分别是正方体ABCD－A1B1C1D1的棱AB、BC、DD1上的点.
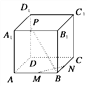
(1)若
，求证：无论点P在DD1上如何移动，总有BP⊥MN；
(2)棱DD1上是否存在这样的点P，使得平面APC1⊥平面ACC1？证明你的结论.
【答案】（1）证明见解析；（1）存在点P，证明见解析；
【解析】解：（1）证明：连AC，BD，在△ABC中，
∵＝，∴MN∥AC.
又∵AC⊥BD，DD1⊥底面ABCD.
∴DD1⊥AC，故AC⊥平面BDD1B1.
进而MN⊥平面BDD1B1，
∵BP面BDD1B1，
∴MN⊥BP.
（2）假设存在点P，使面APC1⊥面ACC1，过P作PF⊥AC1，则PF⊥面ACC1.
又∵BD⊥面ACC1，∴PF∥BD，而两平行线PF、BD所确定的平面即为两相交直线BD、DD1确定的对角面BB1D1D，
∴F为AC1与对角面BB1D1D的交点，
故F为AC1的中点，由PF∥BD，P∈DD1知，P也是DD1的中点．
显然，当P为DD1中点，F为AC1中点时，
∵AP＝PC1，∴PF⊥AC1
又PF∥BD，BD⊥AC，∴PF⊥AC.
从而PF⊥面ACC1，则面APC1⊥面ACC1.
故存在点P，使P为DD1中点时，面APC1⊥面ACC1.
练习册系列答案
相关题目
