题目内容
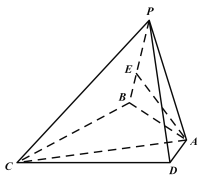
【题目】如图,在四棱锥![]() 中,
中,![]() 是等边三角形,
是等边三角形,![]() ,
,![]() ,
,![]() .
.
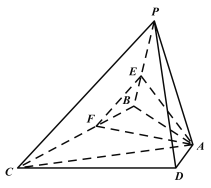
(1)若![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(2)若![]() ,则在线段
,则在线段![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 平面
平面![]() .若存在,求线段
.若存在,求线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]()
【解析】
(1)由![]() 得
得![]() ,再证
,再证![]() 平面
平面![]() ,即可计算出三棱锥
,即可计算出三棱锥![]() 的体积;
的体积;
(2)当![]() 是
是![]() 的三等分点时,满足条件. 作
的三等分点时,满足条件. 作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,可证明
,可证明![]() ,进而证明平面
,进而证明平面![]() 平面
平面![]() .
.
(1)因为![]() 是等边三角形,
是等边三角形,![]() ,所以
,所以![]() .又因为
.又因为![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
所以三棱锥![]() 的体积
的体积![]() ;
;
(2)在线段![]() 上存在一点
上存在一点![]() ,使平面
,使平面![]() 平面
平面![]() .此时
.此时![]() .
.
理由如下:
如图,作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,
,
因为![]() ,所以
,所以![]() 是
是![]() 的三等分点,可得
的三等分点,可得![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因为 ,所以
,所以![]() ,所以
,所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
所以在线段![]() 上存在一点
上存在一点![]() ,使平面
,使平面![]() 平面
平面![]() .此时
.此时![]() .
.

【题目】跨年迎新联欢晚会简称跨年晚会,是指每年阳历年末12月31日晚上各电视台和政府为喜迎新而精心策划的演唱会活动,跨年晚会首次出现在港台地区,跨年晚会因形式和举办地不同因而名称也不同,如央视启航2020跨年盛典,湖南卫视跨年演唱会,东方卫视迎新晚会等.某电视台为了了解2020年举办的跨年迎新晚会观众的满意度,现分别随机选出![]() 名观众对迎新晚会的质量评估评分,最高分为
名观众对迎新晚会的质量评估评分,最高分为![]() 分,综合得分情况如下表所示:
分,综合得分情况如下表所示:
综合得分 |
|
|
|
|
|
|
|
观众人数 | 5 | 10 | 25 | 30 | 15 | 10 | 5 |
根据表中的数据,回答下列问题:
(1)根据表中的数据,绘制这![]() 位观众打分的频率分布直方图;
位观众打分的频率分布直方图;
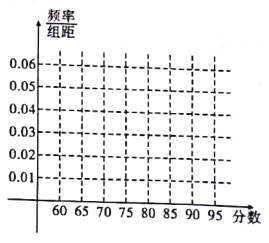
(2)已知观众的评分![]() 近似服从
近似服从![]() ,其中
,其中![]() 是反应随机变量
是反应随机变量![]() 取值的平均水平的特征数,工作人员在分析数据时发现,可用
取值的平均水平的特征数,工作人员在分析数据时发现,可用![]() 位观众评分的平均数估计
位观众评分的平均数估计![]() ,但由于评分观众人数较少,误差较大,所以不能直接用
,但由于评分观众人数较少,误差较大,所以不能直接用![]() 位观众评分的标准差的值估计
位观众评分的标准差的值估计![]() ,而在这
,而在这![]() 位观众打分的频率分布直方图的基础上依据
位观众打分的频率分布直方图的基础上依据![]() 来估计
来估计![]() 更科学合理,试求
更科学合理,试求![]() 和
和![]() 的估计值(
的估计值(![]() 的结果精确到小数点后两位).
的结果精确到小数点后两位).
【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:

等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 | a | 24 | b |
(1)由该题中频率分布直方图求测试成绩的平均数和中位数;
(2)其他条件不变在评定等级为“合格”的学生中依次抽取2人进行座谈,每次抽取1人,求在第1次抽取的测试得分低于80分的前提下,第2次抽取的测试得分仍低于80分的概率;
(3)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.