题目内容
【题目】已知三棱锥
底面的3个顶点
在球
的同一个大圆上，且
为正三角形，
为该球面上的点，若三棱锥体积的最大值为
，则球的表面积为( )
A. 
B. 
C. 
D. 
【答案】B
【解析】
由题意正三棱锥P﹣ABC的四个顶点都在同一球面上，从而三角形ABC的中心就是球心O，PO是球的半径，也是正三棱锥的高，利用正三棱锥P﹣ABC求得球的半径，即可求出球O的表面积．
正三棱锥P﹣ABC的四个顶点都在同一球面上，
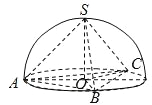
其中底面的三个顶点在该球的一个大圆上．因为题目中涉及到体积最大值，故ABC的中心就是球心O，PO是球的半径，也是正三棱锥的高，设为R，
底面三角形的边长设为a，由正弦定理得到
，三角形的面积为
，椎体的体积为
则球O的表面积是4πR2=4π×4=16π．
故答案为：B
【题目】进入冬天，大气流动性变差，容易形成雾握天气，从而影响空气质量．某城市环保部门试图探究车流量与空气质量的相关性，以确定是否对车辆实施限行．为此，环保部门采集到该城市过去一周内某时段车流量与空气质量指数的数据如下表：
时间 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
车流量（x万辆） | 10 | 9 | 9.5 | 10.5 | 11 | 8 | 8.5 |
空气质量指数y | 78 | 76 | 77 | 79 | 80 | 73 | 75 |
（1）根据表中周一到周五的数据，求
关于
的线性回归方程；
（2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2，则认为得到的线性回归方程是可靠的．请根据周六和周日数据，判定所得的线性回归方程是否可靠？
附：回归方程
中斜率和截距最小二乘估计公式分别为：
其中：
【题目】有一名高二学生盼望2020年进入某名牌大学学习，假设该名牌大学有以下条件之一均可录取：①2020年2月通过考试进入国家数学奥赛集训队（集训队从2019年10月省数学竞赛一等奖中选拔）；②2020年3月自主招生考试通过并且达到2020年6月高考重点分数线，③2020年6月高考达到该校录取分数线（该校录取分数线高于重点线），该学生具备参加省数学竞赛、自主招生和高考的资格且估计自己通过各种考试的概率如下表
省数学竞赛一等奖 | 自主招生通过 | 高考达重点线 | 高考达该校分数线 |
0.5 | 0.6 | 0.9 | 0.7 |
若该学生数学竞赛获省一等奖，则该学生估计进入国家集训队的概率是0.2.若进入国家集训队，则提前录取，若未被录取，则再按②、③顺序依次录取：前面已经被录取后，不得参加后面的考试或录取.（注：自主招生考试通过且高考达重点线才能录取）
（1）求该学生参加自主招生考试的概率；
（2）求该学生参加考试的次数
的分布列及数学期望；
