题目内容
【题目】定义区间
、
、
、
的长度均为
，已知不等式
的解集为
.
（1）求的长度；
（2）函数
（
，
）的定义域与值域都是（
），求区间的最大长度；
（3）关于
的不等式
的解集为
，若
的长度为6，求实数
的取值范围.
【答案】（1）
；（2）
；（3）
.
【解析】
解不等式得其解集即得区间长度.(2) 由题意求出f（x）的定义域并化简解析式，判断出
区间的范围和f（x）的单调性，由题意列出方程组，转化为m，n是方程f（x）的同号的相
异实数根，利用韦达定理表示出mn和m+n，由判别式大于零求出a 的范围，表示出n﹣m
利用配方法化简后，由二次函数的性质求出最大值和a的值．(3)先求出A∩B（0，6），再
转化为不等式组
，当x∈（0，6）时恒成立. 分析两个恒成立问题即得t
的取值范围.
解不等式
得其解为-1≤x＜6，所以解集A区间长度为6-(-1)=7.
(2) 由题意得，函数f（x）的定义域是{x|x≠0}，
∵[m，n]是其定义域的子集，∴[m，n]（﹣∞，0）或（0，+∞）．
∵f（x）=
在[m，n]上是增函数，
∴由条件得
，则m，n是方程f（x）=x的同号相异的实数根，
即m，n是方程（ax）2﹣（a2+a）x+1=0同号相异的实数根．
∴mn=
，m+n=
=
，
则△=（a2+a）2﹣4a2＞0，解得a＞1或a＜﹣3．
∴n﹣m=
=
=
=
，
∴n﹣m的最大值为，此时
，解得a=3.
即在区间[m，n]的最大长度为．
(3) 因为x>0,A=[-1,6），
的长度为6，所以A∩B（0，6）.
不等式log2x+log2（tx+3t）＜2等价于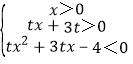
又A∩B（0，6），不等式组的解集的各区间长度和为6，所以不等式组，
当x∈（0，6）时恒成立.
当x∈（0，6）时，不等式tx+3t＞0恒成立，得t＞0
当x∈（0，6）时，不等式tx2+3tx﹣4＜0恒成立，即
恒成立
当x∈（0，6）时，
的取值范围为
，所以实数
综上所述，t的取值范围为
名校课堂系列答案
