��Ŀ����
10����ƽ��ֱ������ϵxOy��ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ��ԲC��Բ��C�ļ�����Ϊ��$\sqrt{2}$��$\frac{��}{4}$�����뾶r=$\sqrt{2}$����1���ڼ�����ϵ�У�ֱ�ߦ�=$\frac{��}{3}$���ѡ�R����ԲC�������㣬�������ľ��룻
��2����ֱ������ϵxOy�У���ԲC�ڵĶ���M��1��0����ֱ��l��ֱ��l��ԲC����A��B���㣬��ֱ��l����б��Ϊ����������AB�е�N�Ĺ켣���̣�
���� ��1�����ԲC�ġ�ֱ�ߵ�ֱ�����귽�̣�����Բ�ĵ�ֱ�ߵľ��룬���ù��ɶ����������ľ��룻
��2����ֱ��l����б��Ϊ�ȣ��������⣬��MCN=�ȣ�CN=cos�ȣ����������AB�е�N�Ĺ켣���̣�
��� 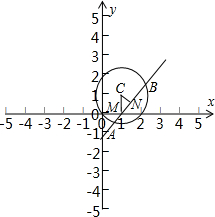 �⣺��1��ԲC��Բ��C�ļ�����Ϊ��$\sqrt{2}$��$\frac{��}{4}$�����뾶r=$\sqrt{2}$��ֱ�����귽��Ϊ��x-1��2+��y-1��2=2��
�⣺��1��ԲC��Բ��C�ļ�����Ϊ��$\sqrt{2}$��$\frac{��}{4}$�����뾶r=$\sqrt{2}$��ֱ�����귽��Ϊ��x-1��2+��y-1��2=2��
ֱ�ߦ�=$\frac{��}{3}$���ѡ�R����ֱ�����귽��Ϊy=$\sqrt{3}$x��
Բ�ĵ�ֱ�ߵľ���Ϊ$\frac{|\sqrt{3}-1|}{\sqrt{3+1}}$=$\frac{\sqrt{3}-1}{2}$��
�������ľ���Ϊ2$\sqrt{2-��\frac{\sqrt{3}-1}{2}��^{2}}$=$\frac{\sqrt{3}+1}{2}$��
��2����ֱ��l����б��Ϊ�ȣ��������⣬��MCN=�ȣ�CN=cos��
��N��x��y������x=1+CNsin��=1+cos��sin�ȣ�y=1-cos2�ȣ�
����AB�е�N�Ĺ켣����Ϊ$\left\{\begin{array}{l}{x=1+cos��sin��}\\{y=1-co{s}^{2}��}\end{array}\right.$��
���� ���⿼�鼫������ֱ�����귽�̵Ļ���������ѧ���ļ�����������ȷת���ǹؼ���

��ϰ��ϵ�д�
�����Ŀ
11������Բ�ķ���Ϊ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��b��$\frac{\sqrt{3}}{2}$a��0���ҽ���ΪF��c��0����c��0��������ax2+bx-c=0����ʵ���ֱ�Ϊx1��x2����x12+x22��ȡֵ��Χ�ǣ�������
| A�� | ��0��$\frac{3}{2}$] | B�� | ��1��$\frac{3}{2}$] | C�� | ��1��$\frac{3}{4}$] | D�� | ��1��$\frac{7}{4}$] |
5�����Ϊ�ȱ������ε�ֱ���������ΪV����ô��������Сʱ������߳�Ϊ��������
| A�� | $\root{3}{4V}$ | B�� | $\root{3}{6V}$ | C�� | $\root{3}{8V}$ | D�� | $\sqrt{4V}$ |
15�� ��ͼ��������A1B1C1-ABC�У�����AA1�͵���ABC������������ABC���������Σ�E��BC�е㣬������������ȷ���ǣ�������
��ͼ��������A1B1C1-ABC�У�����AA1�͵���ABC������������ABC���������Σ�E��BC�е㣬������������ȷ���ǣ�������
 ��ͼ��������A1B1C1-ABC�У�����AA1�͵���ABC������������ABC���������Σ�E��BC�е㣬������������ȷ���ǣ�������
��ͼ��������A1B1C1-ABC�У�����AA1�͵���ABC������������ABC���������Σ�E��BC�е㣬������������ȷ���ǣ�������| A�� | AC��ƽ��ABB1A1 | B�� | CC1��B1E������ֱ�� | ||
| C�� | A1C1��B1E | D�� | AE��BB1 |
19�� ��֪����f��x��=sin����x+�գ����أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����y=f��x����ͼ�����y=cos2xͼ������
��֪����f��x��=sin����x+�գ����أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����y=f��x����ͼ�����y=cos2xͼ������
 ��֪����f��x��=sin����x+�գ����أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����y=f��x����ͼ�����y=cos2xͼ������
��֪����f��x��=sin����x+�գ����أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����y=f��x����ͼ�����y=cos2xͼ������| A�� | ����ƽ��$\frac{��}{3}$�����ȵ�λ | B�� | ����ƽ��$\frac{��}{3}$�����ȵ�λ | ||
| C�� | ����ƽ��$\frac{��}{6}$�����ȵ�λ | D�� | ����ƽ��$\frac{��}{6}$�����ȵ�λ |
 ��ͼ����������ABCD-A1B1C1D1�У�E��F�ֱ���BB1��CD���е㣮
��ͼ����������ABCD-A1B1C1D1�У�E��F�ֱ���BB1��CD���е㣮 ��ͼ������S-ABCD������߳�Ϊ2��PΪ����SD�Ͽ���D�����ȷֵ㣬
��ͼ������S-ABCD������߳�Ϊ2��PΪ����SD�Ͽ���D�����ȷֵ㣬 ��ͼ������P-ABCD�У�AB��AD��AP������ֱ�����ȷֱ�Ϊ1��2��2����$\overrightarrow{DC}$=2$\overrightarrow{AB}$��
��ͼ������P-ABCD�У�AB��AD��AP������ֱ�����ȷֱ�Ϊ1��2��2����$\overrightarrow{DC}$=2$\overrightarrow{AB}$��