题目内容
11.设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b≥$\frac{\sqrt{3}}{2}$a>0)右焦点为F(c,0)(c>0),方程ax2+bx-c=0的两实根分别为x1,x2,则x12+x22的取值范围是( )| A. | (0,$\frac{3}{2}$] | B. | (1,$\frac{3}{2}$] | C. | (1,$\frac{3}{4}$] | D. | (1,$\frac{7}{4}$] |
分析 b≥$\frac{\sqrt{3}}{2}$a>0,可得$\frac{b}{a}≥\frac{\sqrt{3}}{2}$,可得0<$e=\sqrt{1-(\frac{b}{a})^{2}}$≤$\frac{1}{2}$,再利用一元二次方程的根与系数的关系、二次函数的单调性即可得出.
解答 解:∵b≥$\frac{\sqrt{3}}{2}$a>0,∴$\frac{b}{a}≥\frac{\sqrt{3}}{2}$,
∴0<$e=\sqrt{1-(\frac{b}{a})^{2}}$≤$\frac{1}{2}$
∵方程ax2+bx-c=0的两实根分别为x1,x2,△>0,
∴x1+x2=-$\frac{b}{a}$,${x}_{1}{x}_{2}=-\frac{c}{a}$.
则x12+x22=$({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}$=$\frac{{b}^{2}}{{a}^{2}}+\frac{2c}{a}$=$\frac{{a}^{2}-{c}^{2}}{{a}^{2}}$+2e=-e2+2e+1=-(e-1)2+2,
∵$0<e≤\frac{1}{2}$,
∴x12+x22的取值范围是$(1,\frac{7}{4}]$.
故选:D.
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.设直线y=k(x-4)+3是圆x2+y2=9的一条割线,则k的取值一定满足( )
| A. | (-∞,-$\frac{24}{7}$) | B. | (0,$\frac{24}{7}$) | C. | (-$\frac{24}{7}$,0) | D. | (-$\frac{24}{7}$,$\frac{24}{7}$) |
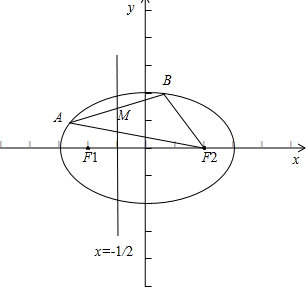 如图,F1,F2是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=-$\frac{1}{2}$上.
如图,F1,F2是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=-$\frac{1}{2}$上. 如图,正方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点.求证:
如图,正方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点.求证: 如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是棱AB,A1D1,AD的中点,求证:
如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是棱AB,A1D1,AD的中点,求证: