Question

1．如图，在正方体ABCD-A₁B₁C₁D₁中，E、F分别是BB₁、CD的中点．
（1）证明：AD⊥D₁F；
（2）证明：面AED⊥面A₁FD₁．

Answer 1

分析 （1）建立空间直角坐标系，利用向量法即可证明：AD⊥D₁F；
（2）利用向量法结合面面垂直的判定定理即可证明：面AED⊥面A₁FD₁．

解答 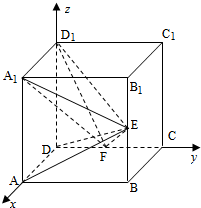解：以D为原点，DA，DC，DD₁为x，y，z轴建立空间直角坐标系．
设正方体的棱长为1…（1分）
则有A（1，0，0），E（1，2，$\frac{1}{2}$），F（0，$\frac{1}{2}$，0），D₁（0，0，1），A₁（1，0，1）…（2分）
（1）$\overrightarrow{AD}$=（-1，0，0），$\overrightarrow{{D}_{1}F}$=（0，$\frac{1}{2}$，-1），
∵$\overrightarrow{AD}•\overrightarrow{{D}_{1}F}=0$，
∴AD⊥D₁F…（6分）
（2）由以上可知D₁F⊥平面AED，
又D₁F在平面A₁FD₁内，
∴面AED⊥面A₁FD₁…（12分）

点评 本题主要考查空间直线垂直和面面垂直的判定，建立空间直角坐标系，利用向量法是解决本题的关键．